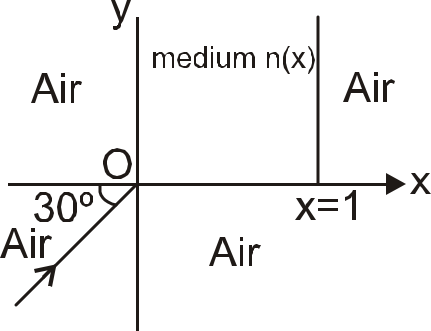
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
DAILY PRACTICE PROBLEM
RESONANCE ENGLISH|Exercise DPP No.40|20 VideosDAILY PRACTICE PROBLEM
RESONANCE ENGLISH|Exercise DPP No.41|9 VideosDAILY PRACTICE PROBLEM
RESONANCE ENGLISH|Exercise DPP No.38|20 VideosCURRENT ELECTRICITY
RESONANCE ENGLISH|Exercise High Level Problems (HIP)|19 VideosELECTRO MAGNETIC WAVES
RESONANCE ENGLISH|Exercise Exercise 3|27 Videos
Similar Questions
Explore conceptually related problems
RESONANCE ENGLISH-DAILY PRACTICE PROBLEM-DPP No.39
- A particle of mass m and charge q is fastened to one end of a string o...
Text Solution
|
- A light ray enters into a medium whose refractive index varies along t...
Text Solution
|
- Four point masses each of mass m are placed on vertices of a regular t...
Text Solution
|
- AB is part of a circuit as shown that absorbs energy at a rate of 50W....
Text Solution
|
- Figure shows a branch/portion of circuit. The electric potential at th...
Text Solution
|
- A wire is bent an an angle theta. A rod of mass m can slide along the ...
Text Solution
|
- A block of mass m = 20 kg is kept is a distance R = 1m from central ax...
Text Solution
|
- A horizontal thin tube of length 2L completely filled with a liquid of...
Text Solution
|
- A horizontal thin tube of length 2L completely filled with a liquid of...
Text Solution
|