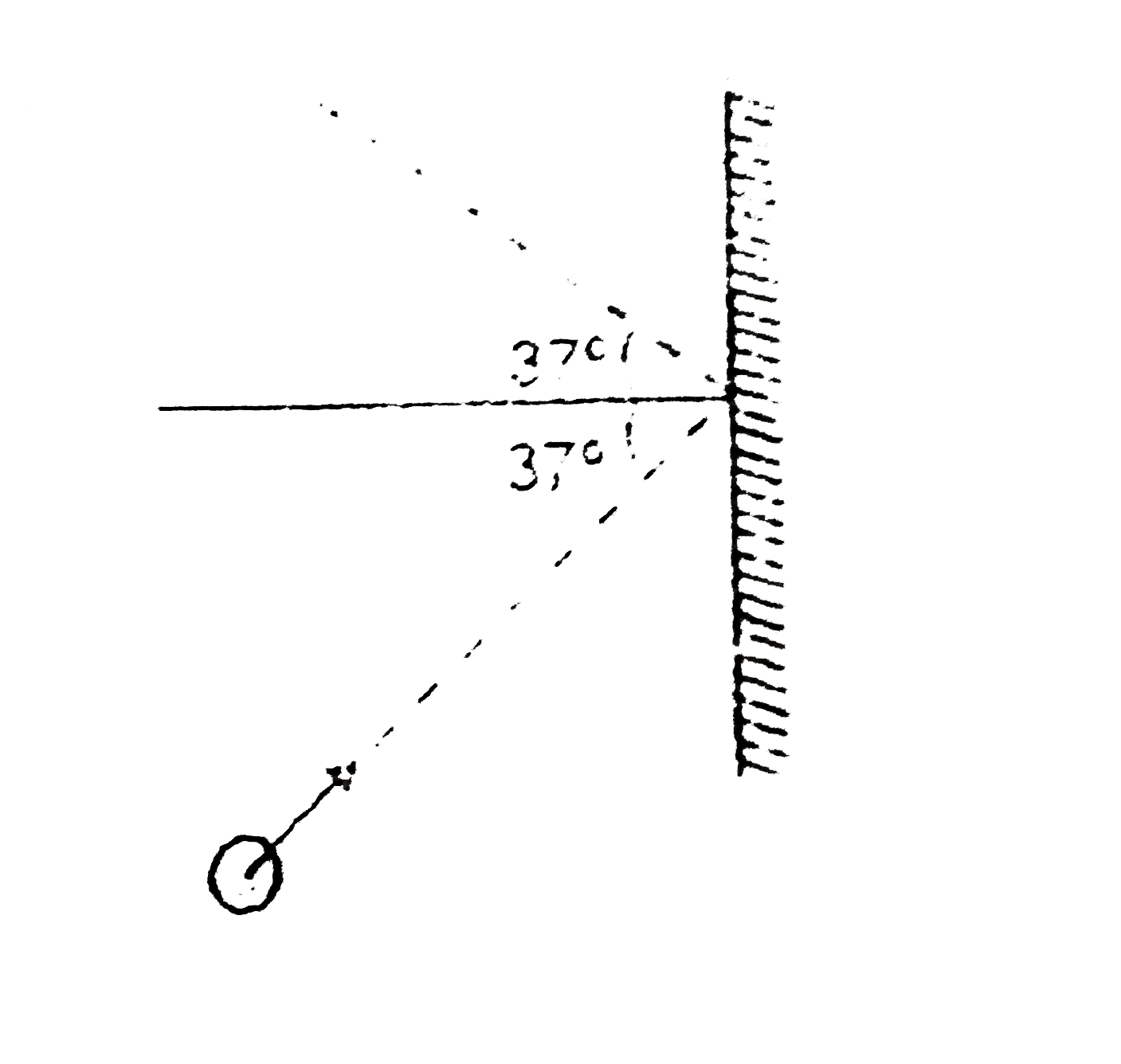
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
DAILY PRACTICE PROBLEM
RESONANCE ENGLISH|Exercise DPP No.60|8 VideosDAILY PRACTICE PROBLEM
RESONANCE ENGLISH|Exercise DPP No.61|20 VideosDAILY PRACTICE PROBLEM
RESONANCE ENGLISH|Exercise DPP No.58|20 VideosCURRENT ELECTRICITY
RESONANCE ENGLISH|Exercise High Level Problems (HIP)|19 VideosELECTRO MAGNETIC WAVES
RESONANCE ENGLISH|Exercise Exercise 3|27 Videos
Similar Questions
Explore conceptually related problems
RESONANCE ENGLISH-DAILY PRACTICE PROBLEM-DPP No.59
- Consider a gravity free hall in which an experimenter of mass 50 kg is...
Text Solution
|
- Two similar bulbs of wattage 100 W//50 sqrt(2)V are connected in circu...
Text Solution
|
- In YDSE, let A and B be two slits. Films of thickness t(A) and t(B) an...
Text Solution
|
- A smooth hemisphere of mass m and radius R is at rest. A smooth solid ...
Text Solution
|
- A charged particle X moves directly towards another charged particle Y...
Text Solution
|
- A particle moving on a smooth horizontal surface strikes a stationary ...
Text Solution
|
- An ideal solenoid of inductance L = 1H. Radius a = 0.5 m and numbers o...
Text Solution
|
- An ideal solenoid of inductance L = 1H. Radius a = 0.5 m and numbers o...
Text Solution
|
- An ideal solenoid of inductance L = 1H. Radius a = 0.5 m and numbers o...
Text Solution
|