Home
Class 11
PHYSICS
Two blocks A and B of masses m and 2m, r...

Two blocks A and B of masses m and 2m, respectively , are held at rest such that the spring is in natural length. Find out the acceleration of both the blocks just after relese.

A

`gdarr g darr`

B

`g/3 darr,g/3 uarr`

C

`0,0`

D

`g darr ,0`

Text Solution

Verified by Experts

The correct Answer is:
A
In this case spring force is zero initially F.B.D. of A and B
Promotional Banner

Topper's Solved these Questions

  • MAGNETIC FIELD AND FORCES

    RESONANCE ENGLISH|Exercise Exercise|64 Videos

  • NUCLEAR PHYSICS

    RESONANCE ENGLISH|Exercise Exercise|35 Videos

Similar Questions

Explore conceptually related problems

Two blocks A and B of masses in and 2m , respectively, are connected with the help of a spring having spring constant, k as shown in Fig. Initially, both the blocks arc moving with same velocity v on a smooth horizontal plane with the spring in its natural length. During their course of motion, block B makes an inelastic collision with block C of mass m which is initially at rest. The coefficient of restitution for the collision is 1//2 . The maximum compression in the spring is

Two blocks 'A' and 'B' having masses m_(A) and m_(a) , respectively are connectd by an arrangement shown in the figure. Calculate the downward acceleration of the block B. Assume the pulleys to be massless. Under what condition will block A have downward acceleration?

Two blocks A and B of same mass m attached with a light spring are suspended by a string as shown in fig. Find the acceleration of block A and B just after the string is cut.

Two block A and B of masses m and 2m respectively are connected by a spring of spring cosntant k. The masses are moving to the right with a uniform velocity v_(0) each, the heavier mass leading the lighter one. The spring is of natural length during this motion. Block B collides head on with a thrid block C of mass 2m . at rest, the collision being completely inelastic. The velocity of block B just after collision is -

Two blocks A and B of masses m and 2m , respectively are connected by a spring of force constant k . The masses are moving to the right with uniform velocity v each, the heavier mass leading the lighter one. The spring is in the natural length during this motion. Block B collides head on with a third block C of mass m , at rest, the collision being completely inelastic. Calculate the maximum compression of the spring.

A block of mass m is suddenly released from the top of a spring of stiffness constant k. a. Find the acceleration of block just after release. b. What is the compression in the spring at equilibrium. c. What is the maximum compression in the spring. d. Find the acceleration of block at maximum compression in the spring.

Two blocks A and B of mass m and 2m respectively are connected by a light spring of force constant k. They are placed on a smooth horizontal surface. Spring is stretched by a length x and then released. Find the relative velocity of the blocks when the spring comes to its natural length

A block A of mass 2m is hanging from a vertical massless spring of spring constant k and is in equilibrium. Another block B of mass m strikes the block A with velocity u and sticks to it as shown in the figure. The magnitude of the acceleration of the combined system of the blocks just after the collision is

Three blocks A, B, and C of masses 3M, 2M , and M are suspended vertically with the help of spring PQ and TU, and a string RS as shown in fig. If the acceleration of blocks A, B and C is a_(1), a_(2) and a_(3) , respectively, then The value of acceleration a_(2) at the moment spring TU is cut is

Three blocks A, B, and C of masses 3M, 2M , and M are suspended vertically with the help of spring PQ and TU, and a string RS as shown in fig. If the acceleration of blocks A, B and C is a_(1), a_(2) and a_(3) , respectively, then The value of acceleration a_(3) at the moment spring PQ is cut is

RESONANCE ENGLISH-NEWTONS LAWS OF MOTION AND FRICTION-Exercise
  1. A body of mass 32 kg is suspended by a spring balance from the roof of...

    Text Solution

    |

  2. There is inclined surface of inclination theta=30^(@). A smooth groove...

    Text Solution

    |

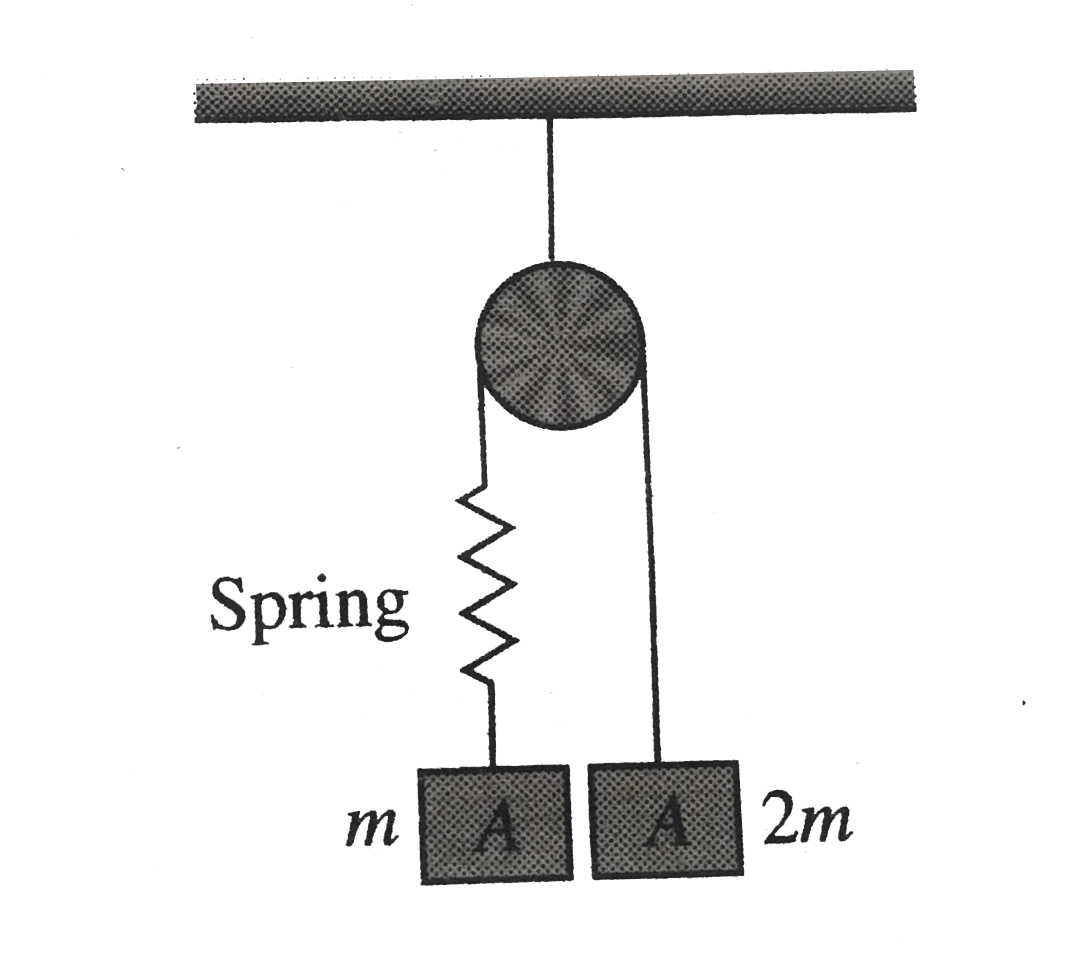
  3. Two blocks A and B of masses m and 2m, respectively , are held at rest...

    Text Solution

    |

  4. A uniform rope of length L and mass M is placed on a smooth fixed wedg...

    Text Solution

    |

  5. A bob is hanging over a pulley inside a car through a string. The seco...

    Text Solution

    |

  6. A spring of negligible mass going over a clamped pulley of mass m supp...

    Text Solution

    |

  7. The system shown is hanging in equilibrium above the ground. When the ...

    Text Solution

    |

  8. Two identical small masses each of mass m are connected by a light ine...

    Text Solution

    |

  9. In the figure, the position time graph of a particle of mass 0.1 kg is...

    Text Solution

    |

  10. A man is standing on a sparing platform, Reading of spring balaance is...

    Text Solution

    |

  11. Figure shows a 5 kg ladder hanging from a string that is connected wit...

    Text Solution

    |

  12. A ball of mass 3kg moving with a speed of 100 m/s, strikes a wall at a...

    Text Solution

    |

  13. A block of mass 4 kg is suspended through two light spring balances A ...

    Text Solution

    |

  14. Two masses m(1) and m(2) which are connected with a light string, are ...

    Text Solution

    |

  15. A wooden block and a metal coin are connected by a string as shown in ...

    Text Solution

    |

  16. Calculate the tension in the string shown in figure. The pulley and th...

    Text Solution

    |

  17. The elevator shown in figure is descending with an acceleration of 2m/...

    Text Solution

    |

  18. In fig., a person wants to rise a block lying on the ground to a heigh...

    Text Solution

    |

  19. Blocks of mass M(1) and M(2) are connected by a cord which passes over...

    Text Solution

    |

  20. A painter of mass M stands on a platforms of mass m and pulls himself ...

    Text Solution

    |