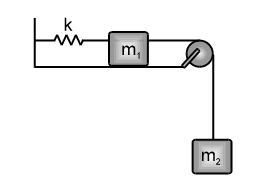
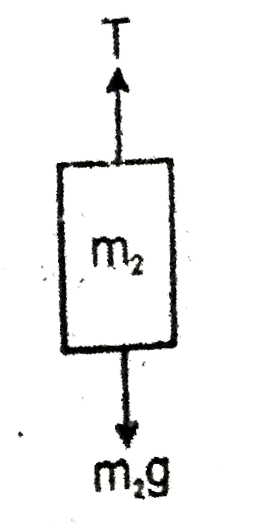
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
RESONANCE ENGLISH-PART TEST 3-Exercise
- Figure shows a rectangular pulse and triangular pulse approaching towa...
Text Solution
|
- A stationary observer receives sonic oscillations from two tuning for...
Text Solution
|
- When two mutually perpendicular simple harmonic motions of same freque...
Text Solution
|
- When two waves of the same amplitude and frequency but having a phase ...
Text Solution
|
- A simple pendulum , a physical pendulum, a torsional pendulum and a sp...
Text Solution
|
- S(1) and S(2) are two coherent sources of sound of frequency 110Hz eac...
Text Solution
|
- A transverse wave of amplitude 5 mm and frequency 10Hz is produced on ...
Text Solution
|
- When a composite wire is made by joining tow wires as shown in figure ...
Text Solution
|
- When the net force F acting on the particle varies as its position al...
Text Solution
|
- The time period of a particle in simple harmonic motion is T. Assume p...
Text Solution
|
- m(1) & m(2)are connected with a light inextensible string with m(1) ly...
Text Solution
|
- A particle is subjected to two simple harmonic motions along x and y d...
Text Solution
|
- A wire of length 'l' having tension T and radius 'r' vibrates with fun...
Text Solution
|
- In a standing wave on a string.
Text Solution
|
- Which of the following statements is correct:
Text Solution
|
- The displacement time graph of a particle executing S.H.M. (in straigh...
Text Solution
|
- The length of the wire shown in figure between the pulley is 1.5 m and...
Text Solution
|
- A force of 6.4 N stretches a vertical spring by 0.1 m. The mass (in kg...
Text Solution
|
- Statement 1: A tuning fork of constant frequency sends sound waves in ...
Text Solution
|
- Statement 1: Sound waves can not propagate through vacuum but light wa...
Text Solution
|