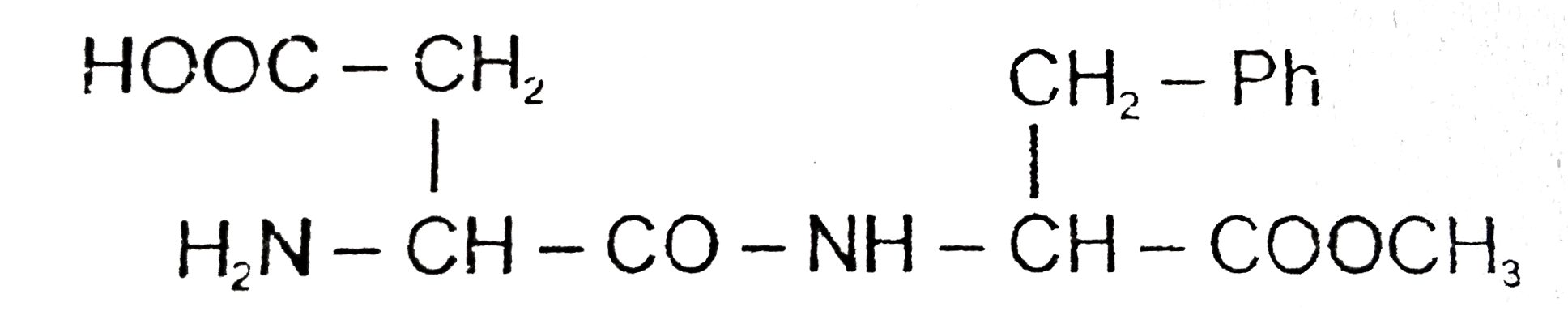A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
BIOMOLECULES
RESONANCE ENGLISH|Exercise Ex-2(More correct)Part-II|14 VideosBIOMOLECULES
RESONANCE ENGLISH|Exercise Ex-2(Comprehension)Part-IV|5 VideosBIOMOLECULES
RESONANCE ENGLISH|Exercise Ex-2(Subjective)Part-I|20 VideosBASIC CONCEPTS
RESONANCE ENGLISH|Exercise ORGANIC CHEMISTRY(BASIC CONCEPTS)|27 VideosBIOMOLECULES & POLYMER
RESONANCE ENGLISH|Exercise ORGANIC CHEMISTRY(Biomolecules & Polymer)|34 Videos
Similar Questions
Explore conceptually related problems
RESONANCE ENGLISH-BIOMOLECULES-Ex-2(Single correct)Part-II
- The density of Carbon dioxide at 7.0 atm pressure and 27^0C is :
Text Solution
|
- The density of Carbon dioxide at 2.0 atm pressure and 27^0C is :
Text Solution
|
- On acid hydrolysis of above disacharide, we get.
Text Solution
|
- Which is correct structure of beta-D-glucopyranose.
Text Solution
|
- The structure of the following polymer is : .
Text Solution
|
- In osazone formation of three molecules of phenylhydrazine which is th...
Text Solution
|
- At 27^(@)C and 4.0 atm pressure, the density of propene gas is :
Text Solution
|
- At 27^(@)C and 6.0 atm pressure, the density of propene gas is :
Text Solution
|
- At 27^(@)C and 2.0 atm pressure, the density of propene gas is :
Text Solution
|
- At 27^(@)C and 5.0 atm pressure, the density of propene gas is :
Text Solution
|
- Aspartame is 160 times as sweet as sucrose and is used as a sugar subs...
Text Solution
|
- The polymerisation reaction shown below 2 CH-= CH overset(CuCl)rarr ...
Text Solution
|
- Which of the following is radical intiator
Text Solution
|
- At 27^(@)C and 7.0 atm pressure, the density of propene gas is :
Text Solution
|
- At 27^(@)C and 8.0 atm pressure, the density of propene gas is :
Text Solution
|
- The rms speed of helium gas at 27^(@)C and 1 atm pressure is 900 ms^(-...
Text Solution
|
- The rms speed of helium gas at 27^(@)C and 1 atm pressure is 800 ms^(-...
Text Solution
|