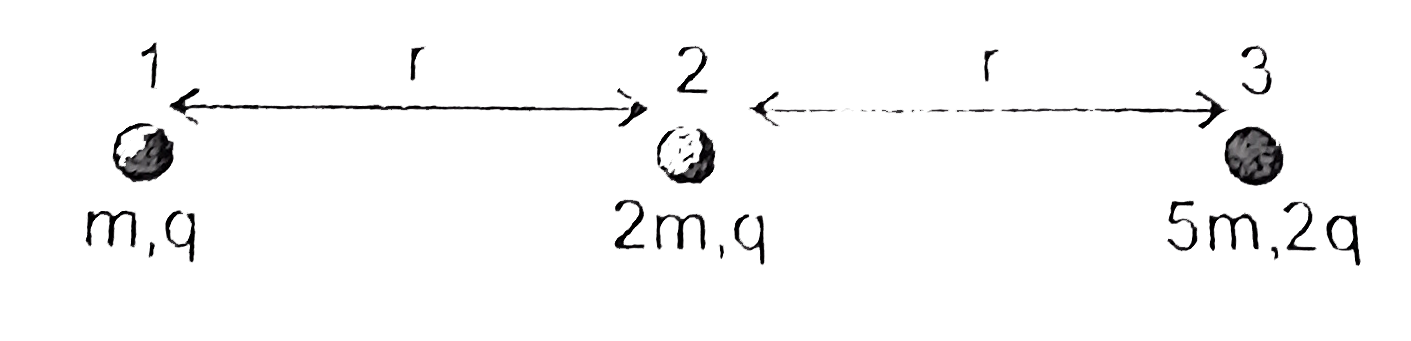A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Three particles having charges q,q and 2q have masses m, 2m and 5 m re...
Text Solution
|
- A charged particle of mass m and charge q is released from rest the po...
Text Solution
|
- An infinte wire having linear charge density lambda is arranged as sho...
Text Solution
|
- Three identical point charges, each of mass m and charge q, hang from ...
Text Solution
|
- A charged particle of mass m and charge q is released from rest in an ...
Text Solution
|
- Two equal positive charges , Q , are fixed at points (0 , d) and (0 , ...
Text Solution
|
- Three particles having charges q,q and 2q have masses m, 2m and 5 m re...
Text Solution
|
- Three particles having charges q,q and 2q have masses m, 2m and 5 m re...
Text Solution
|
- Two charged particles of charge +2q and +q have masses m and 2m respe...
Text Solution
|