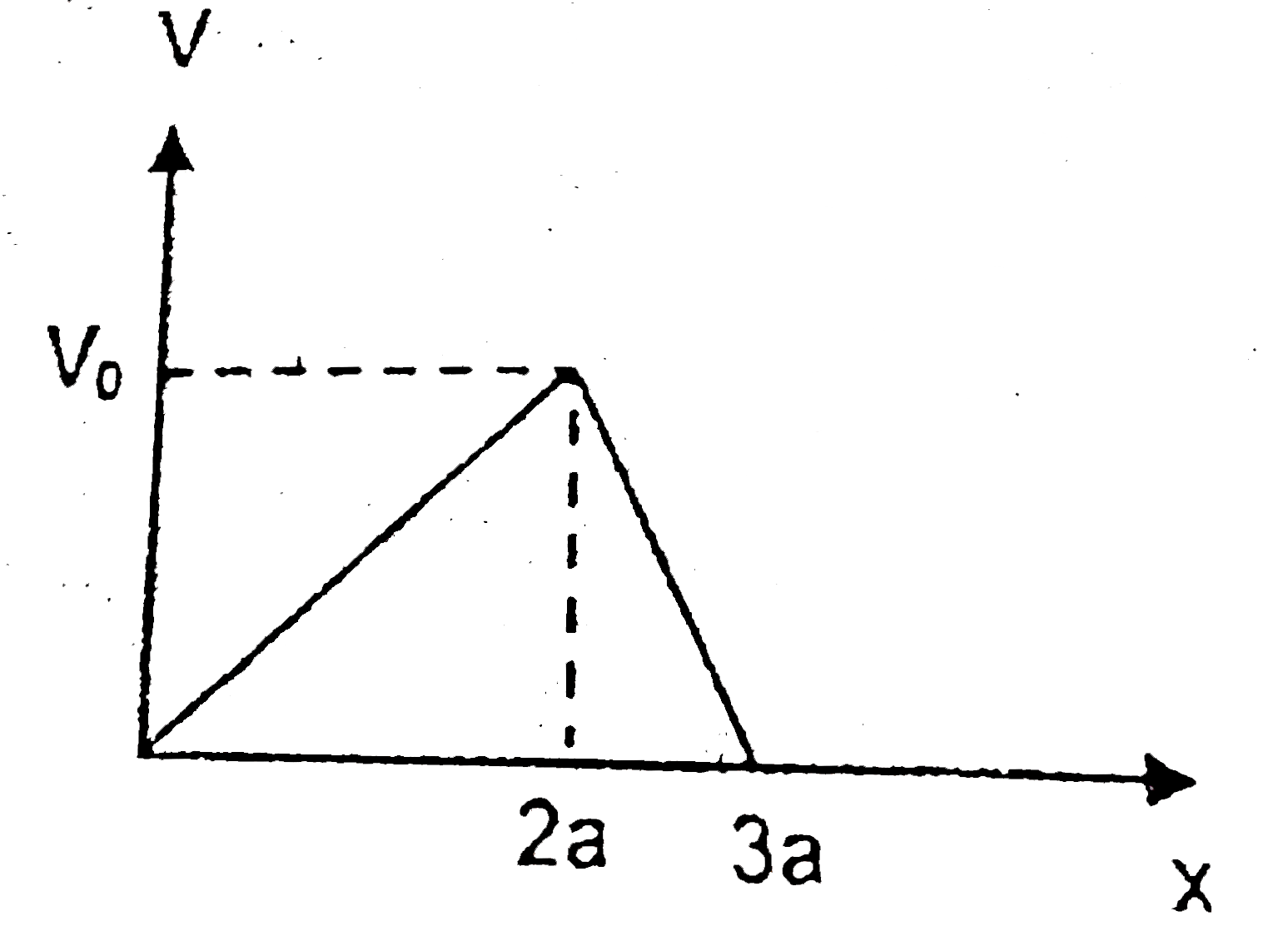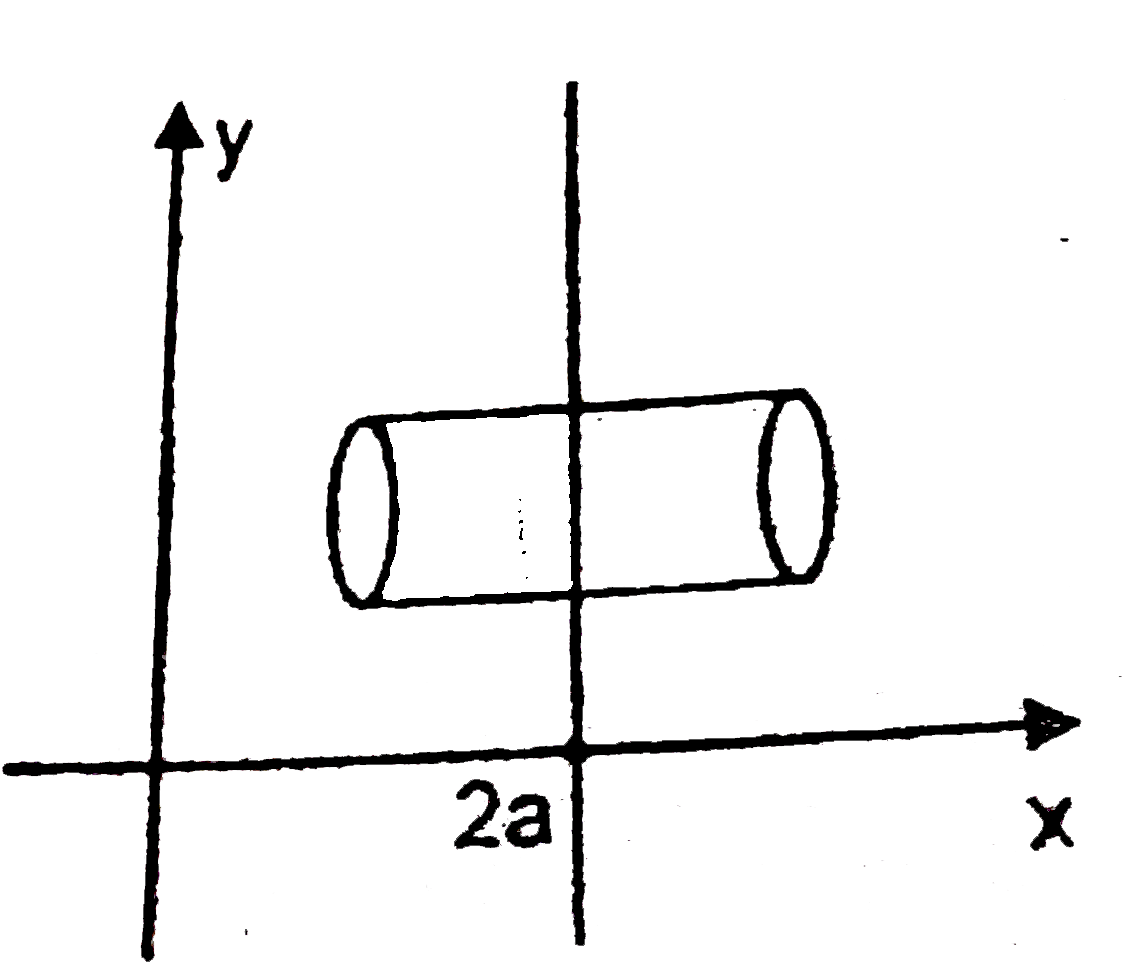A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- There exist electric field in space such that potential gradient along...
Text Solution
|
- The variation of electric potential for an electric field directed par...
Text Solution
|
- A graph of the x-component of the electric field as a function of x in...
Text Solution
|
- There exist electric field in space such that potential gradient along...
Text Solution
|
- A plane electromagnetic wave travels in free space along x-axis. At a ...
Text Solution
|
- Three point charge have been placed along the x axis at points A, B an...
Text Solution
|
- यदि किसी बिन्दु पर विद्युत् विभव V है तो X-अक्ष के अनुदिश उस बिन्दु पर...
Text Solution
|
- An electron is moving along positive x-axis A unifrom electric field e...
Text Solution
|
- An electron is moving along positive x-axis A unifrom electric field e...
Text Solution
|