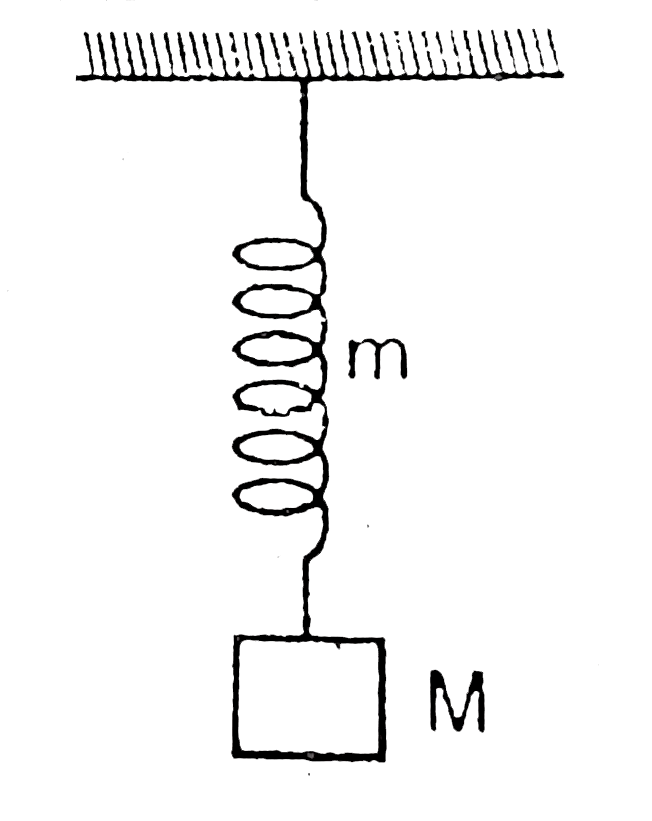A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A block of M is suspended from a vertical spring of mass m as shown in...
Text Solution
|
- A block with a mass of 3.00 kg is suspended from an ideal spring havin...
Text Solution
|
- In the figure shown a block of masss m is atteched at ends of two spri...
Text Solution
|
- When a body of mass 1.0 kg is suspended from a certain light spring ha...
Text Solution
|
- Figure shows a system consisting of a massless pulley, a spring of for...
Text Solution
|
- Blocks A and B shown in the figure are having equal masses m. The syst...
Text Solution
|
- A block of mass m is suspended by different springs of force constant ...
Text Solution
|
- A block of mass m is placed on a smooth block of mass M = m with the h...
Text Solution
|
- The period of oscillation of a mass M suspended from a spring of sprin...
Text Solution
|