A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
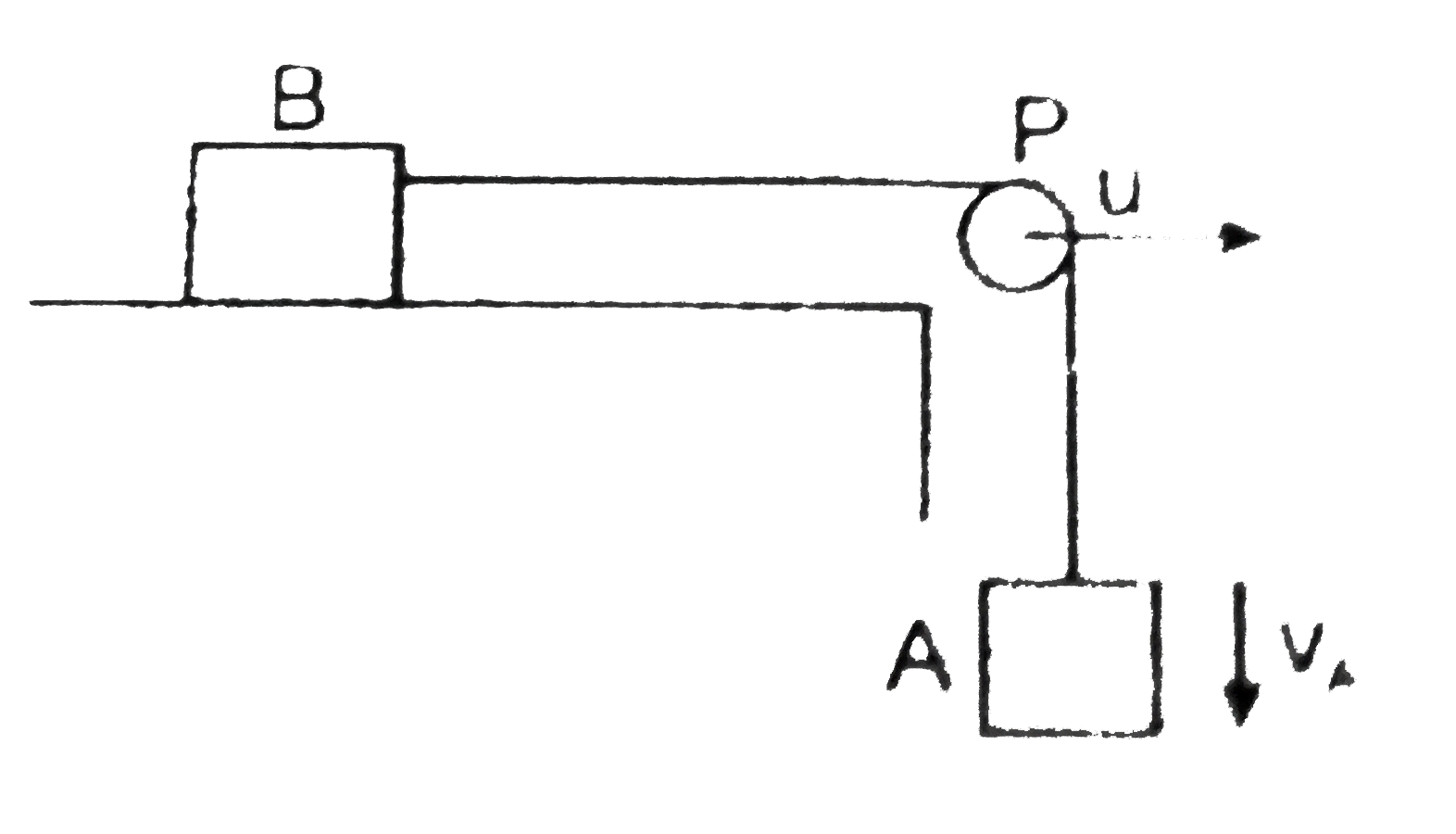
- In the figure the pulley P moves to the right with a constant speed u....
Text Solution
|
- In the arrangement shown in figure the ends P and Q of an inextensible...
Text Solution
|
- The string in fig. is passing over small smooth pulley rigidly attache...
Text Solution
|
- A particle moves in a straight line from A to B with speed v(1) and th...
Text Solution
|
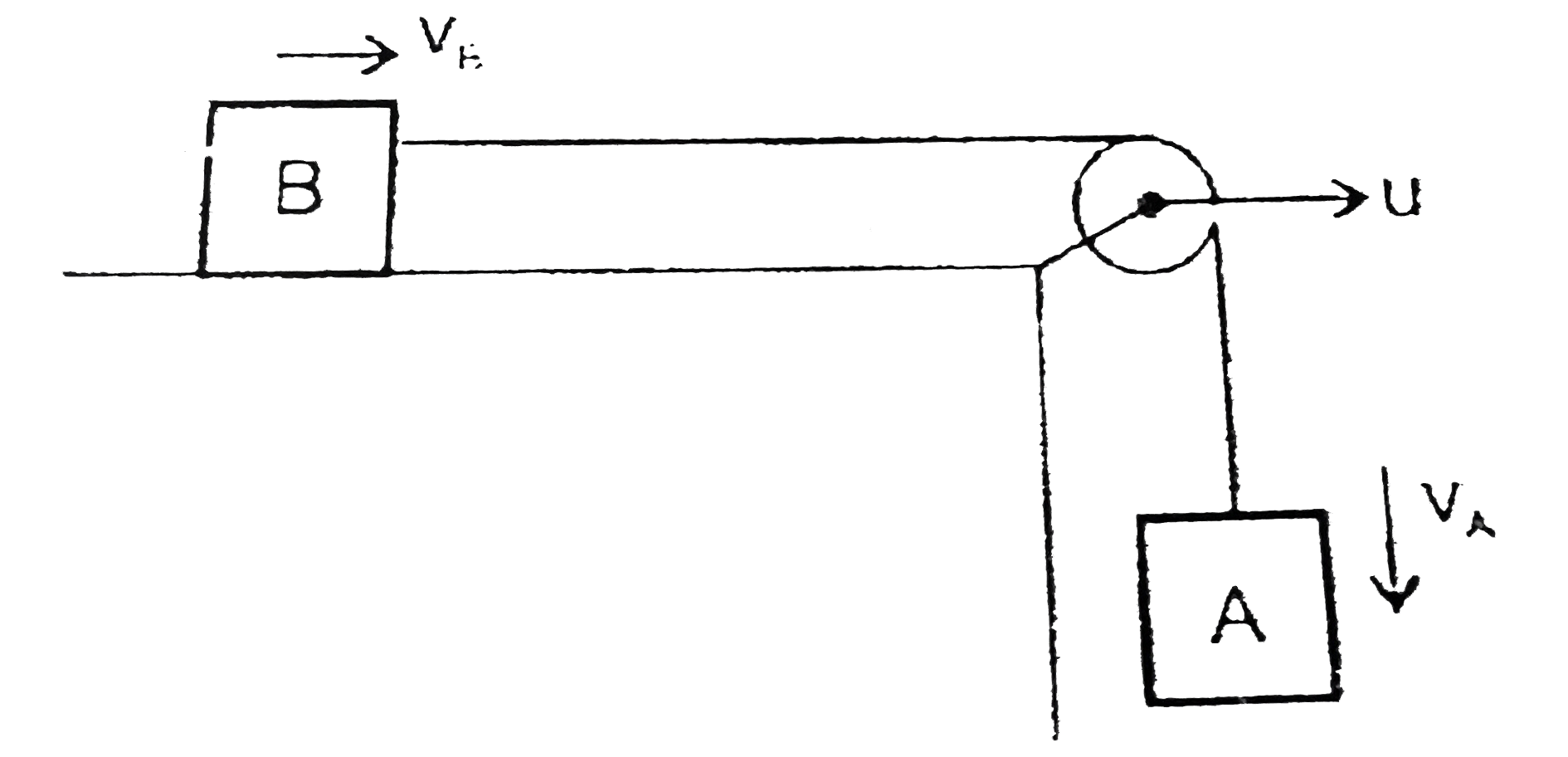
- In the figure, the pulley P moves to the right with a constant speed v...
Text Solution
|
- In the figure, the blocks are of equal mass. The pulley is fixed. In t...
Text Solution
|
- In the figure, the pulley P moves to the right with a constant speed o...
Text Solution
|
- In the figure the pulley P moves to the right with a constant speed u....
Text Solution
|
- In the figure, the pulley P moves to the right with a constant speed u...
Text Solution
|