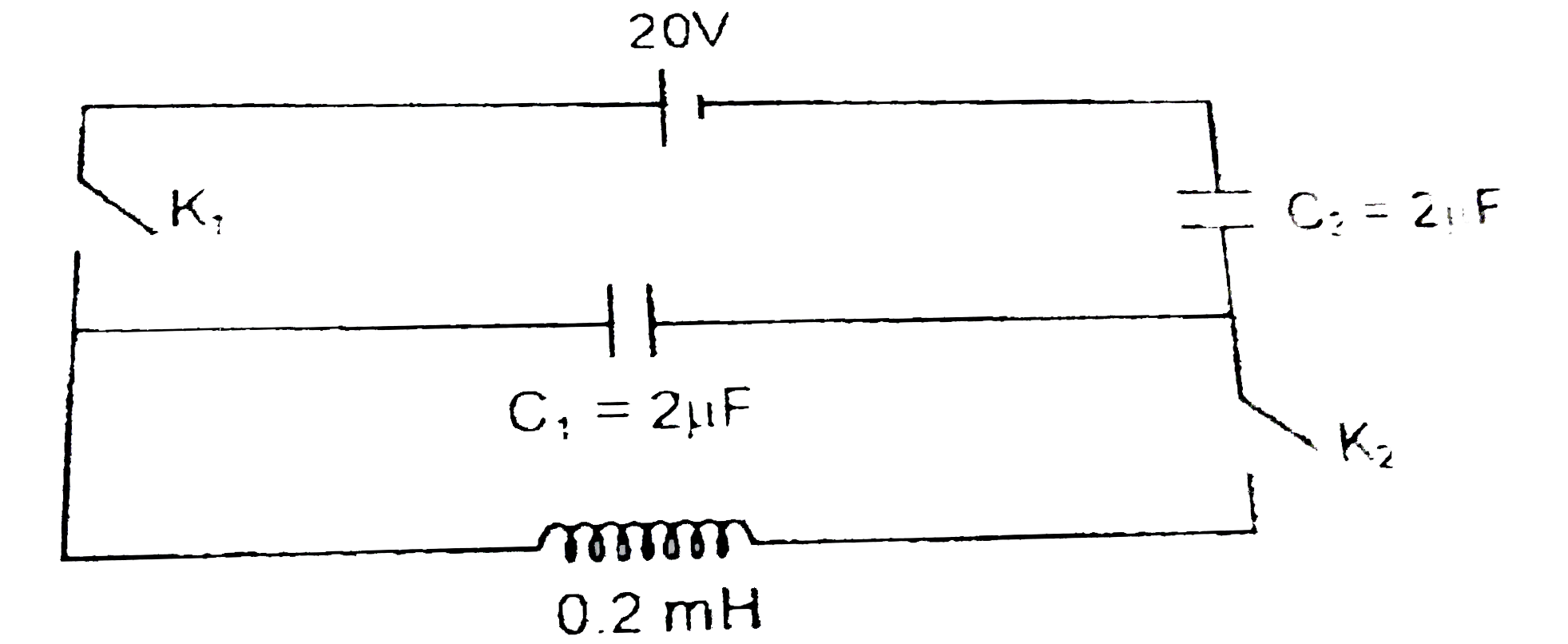A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A circuit containing two capacitor C(1) and C(2) shown in figure is in...
Text Solution
|
- In the circuit shows in Fig. switch k(2) is open and switch k(1) is cl...
Text Solution
|
- A circuit containing capacitors C(1) and C(2) shown in Fig. is in the ...
Text Solution
|
- In the circuit shown in figure , initially key K(1) is closed and key...
Text Solution
|
- In the given circuit, K(1) and K(2) are open initially and the capacot...
Text Solution
|
- In the given circuit, K(1) and K(2) are open initially and the capacot...
Text Solution
|
- In the given circuit, K(1) and K(2) are open initially and the capacot...
Text Solution
|
- In the given circuit, K(1) and K(2) are open initially and the capacot...
Text Solution
|
- A circuit containing capacitors C(1) and C(2) shown in the figure is i...
Text Solution
|