Home
Class 12
PHYSICS
A ring of mass m and radius r rolls with...

A ring of mass m and radius r rolls without slipping on a fixed hemispherical surface of radius R as shown. The time period of small oscillations of ring is `2pisqrt((n(R-r))/(3g))` then find the value of n.

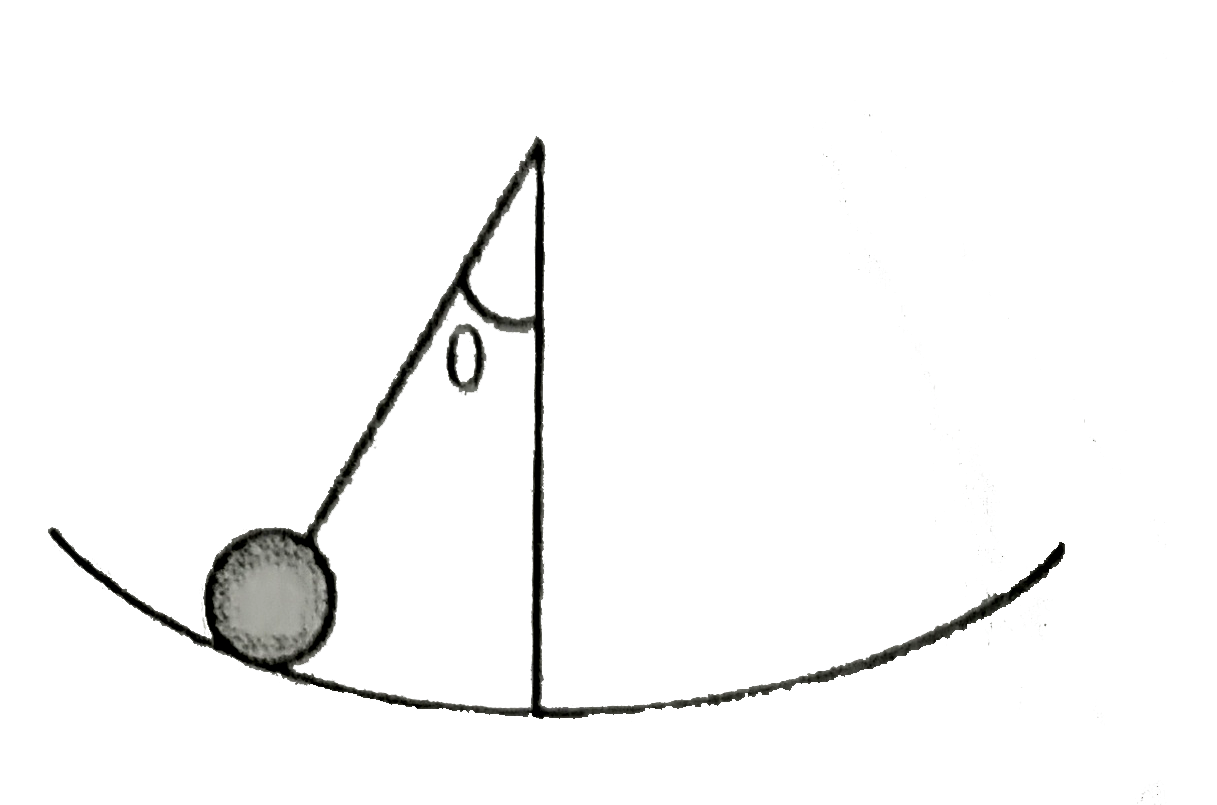
Text Solution

Verified by Experts

The correct Answer is:
6

`mv^(2)+mg(R-r)(1-costheta)=` constant
`implies2mv(dv)/(dt)+mg(R-r)sintheta(dtheta)/(dt)=0`
since `v=omega(R-r)=(-dtheta)/(dt)(R-r)`
`(dv)/(dt)=(-d^(2)theta)/(dt^(2))(R-r)`
`2m(dtheta)/(dt)(R-r)(d^(2)theta)/(dt^(2))(R-r)+mg(R-r)sintheta(dtheta)/(dt)=0`
`implies(d^(2)theta)/(dt^(2))=(-gtheta)/(2(R-r))` (for small `theta,sintheta=0`)
`impliesT=2pisqrt((2(R-r))/(g))`
Promotional Banner

Similar Questions

Explore conceptually related problems

A solid sphere (radius = R) rolls without slipping in a cylindrical throuh (radius = 5R) . Findthe time period of small oscillations.

A solid cylinder of mass M and radius R rolls without slipping on a flat horizontal surface. Its moment of inertia about the line of contact is

A spherical ball of mass m and radius r rolls without slipping on a rough concave surface of large radius R. It makes small oscillations about the lowest point. Find the time period.

A small block oscillates back and forth on as smooth concave surface of radius R in figure. Find the time period of small oscillation.

A sphere of radius r is rolling without slipping on a hemispherical surface of radius R . Angular velocity and angular acceleration of line OA is omega and alpha respectively. Find the acceleration of point P on sphere.

A small ball of radius r rolls without sliding in a big hemispherical bowl. of radius R. what would be the ratio of the translational and rotaional kinetic energies at the bottom of the bowl.

A solid sphere of (radius = R ) rolls without slipping in a cylindrical vessel (radius = 5R ). Find the time period of small of oscillations of the sphere in s^(-1) . Take R = (1)/(14)m and g = 10 m//s^(2) . (axis is cylinder is fixed and horizontal).

For a uniform ring of mass M and radius R at its centre

A drum of radius R and mass M, rolls down without slipping along an inclined plane of angle theta . The frictional force-

A ring of mass m and radius R rolls on a horizontal roudh surface without slipping due to an applied force 'F' . The frcition force acting on ring is :-