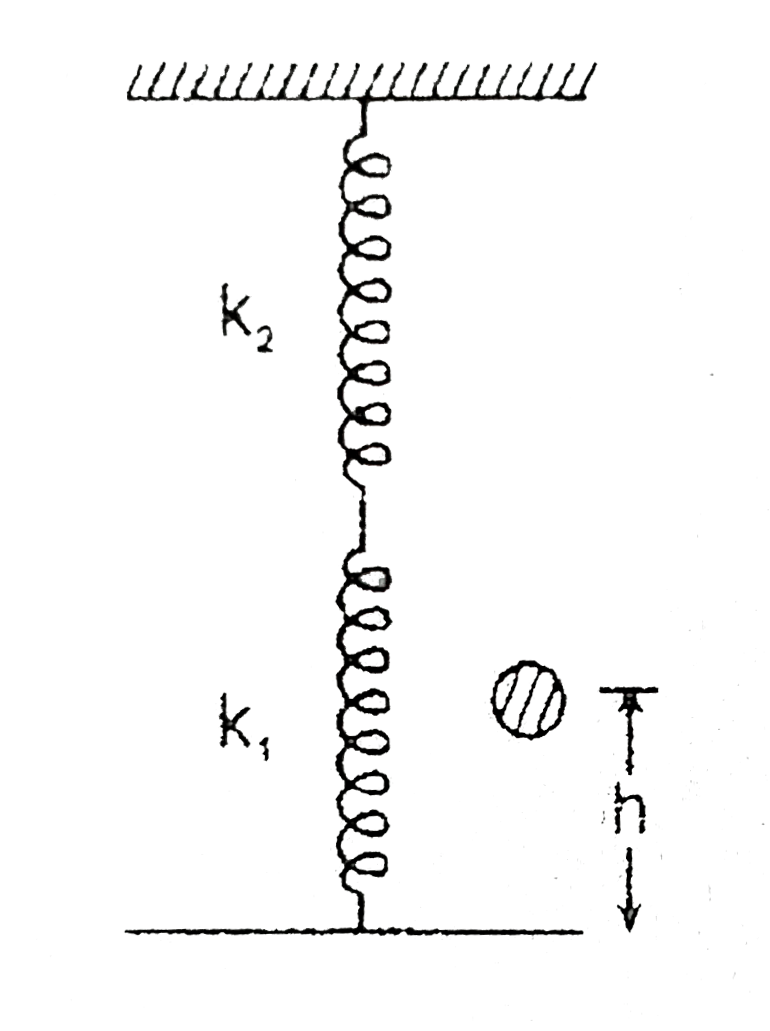Text Solution
Verified by Experts
Topper's Solved these Questions
ELASTICITY AND VISCOCITY
RESONANCE ENGLISH|Exercise Exercise- 1 PART - I|8 VideosELASTICITY AND VISCOCITY
RESONANCE ENGLISH|Exercise Exercise- 1 PART - II|14 VideosDAILY PRACTICE PROBLEMS
RESONANCE ENGLISH|Exercise dpp 92 illustration|2 VideosELECTROMAGNETIC INDUCTION
RESONANCE ENGLISH|Exercise Exercise|43 Videos
Similar Questions
Explore conceptually related problems
RESONANCE ENGLISH-ELASTICITY AND VISCOCITY-Advanced Level Problems
- Hanger is mass less a ball of mass m drops a height h which sticks to ...
Text Solution
|
- A wire loaded by a weight of density 7.8 g//c c is found to be of leng...
Text Solution
|
- Two long metallic strips are joined together by two rivets each of rad...
Text Solution
|
- Eight rain drops of radius 1mm each falling downwards with a terminal ...
Text Solution
|
- An air bubble of 1 cm radius is rising at a steady rate of 2.00ms^-1 t...
Text Solution
|
- Two rods ' A ' & ' B ' of equal free length hang vertically 60 cm apar...
Text Solution
|
- The length of a rod is 20 cm and area of cross-section 2 cm^(2). The Y...
Text Solution
|
- A cylinder of 150 mm radius rotates concentrically inside a fixed cyli...
Text Solution
|
- In a ring having linear charge density lambda, made up of wire of cros...
Text Solution
|
- A thin rod of negligible mass and area of corss-section 2xx10^(-6)m^(2...
Text Solution
|
_S01_010_Q01.png)