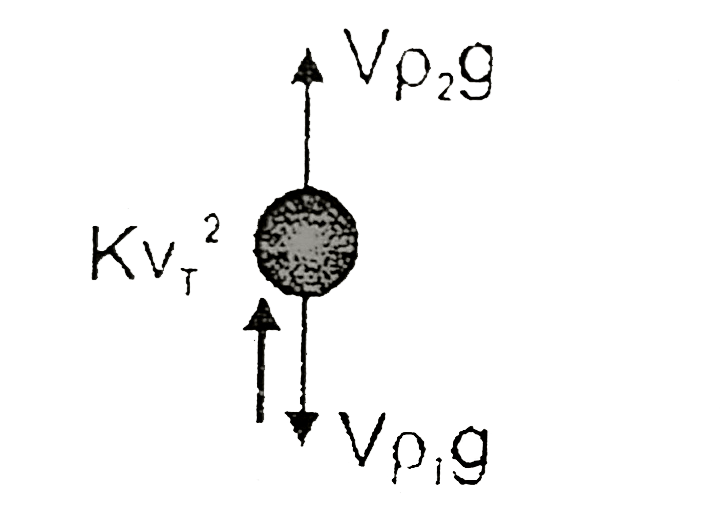
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
ELASTICITY AND VISCOCITY
RESONANCE ENGLISH|Exercise Advanced Level Problems|9 VideosELASTICITY AND VISCOCITY
RESONANCE ENGLISH|Exercise Exercise- 3 PART - I|7 VideosDAILY PRACTICE PROBLEMS
RESONANCE ENGLISH|Exercise dpp 92 illustration|2 VideosELECTROMAGNETIC INDUCTION
RESONANCE ENGLISH|Exercise Exercise|43 Videos
Similar Questions
Explore conceptually related problems
RESONANCE ENGLISH-ELASTICITY AND VISCOCITY-Exercise- 3 PART - IV
- Spherical balls of radius R are falling in a viscous fluid of velocity...
Text Solution
|
- If S is stress and Y is Young's modulus of material of a wire, the ene...
Text Solution
|
- If the terminal speed of a sphere of gold (of density 19.5 g//cm ^3 ) ...
Text Solution
|
- A wire elongates by l mm when a load W is hanged from it if the wire g...
Text Solution
|
- A spherical solid ball of volume V is made of a material of density rh...
Text Solution
|
- Two wires are made of the same material and have the same volume .The...
Text Solution
|
- If a ball of steel density (rho=7.8gcm^(-3)) attains a terminal veloci...
Text Solution
|
- The pressure that has to be applied to the ends of a steel wire of l...
Text Solution
|
- A pendulum made of a uniform wire of cross sectional area A has time T...
Text Solution
|