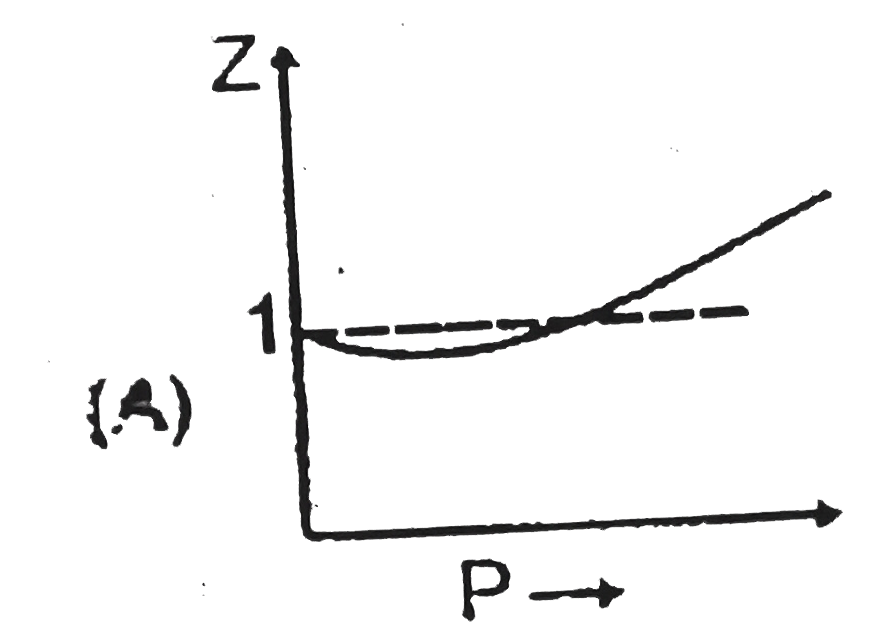
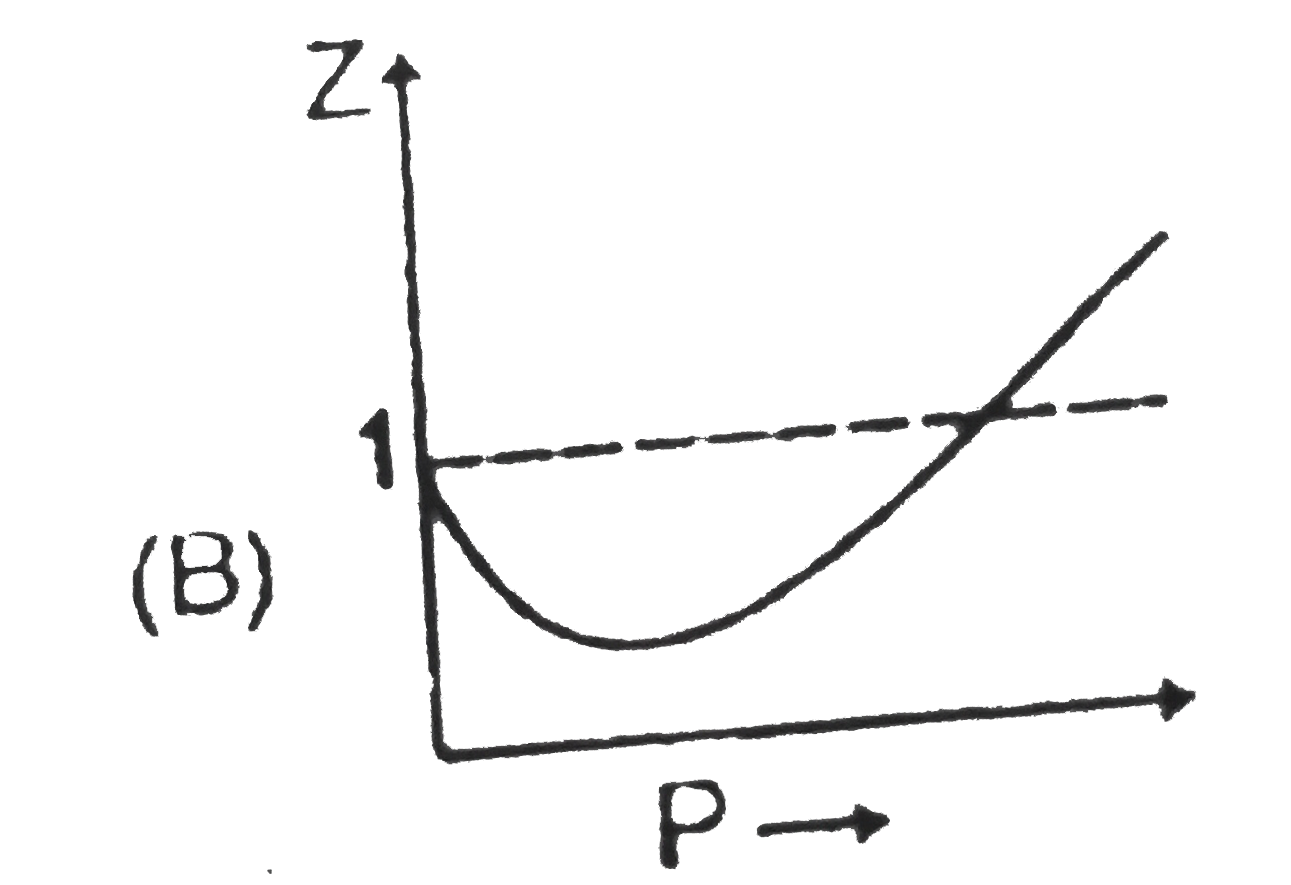
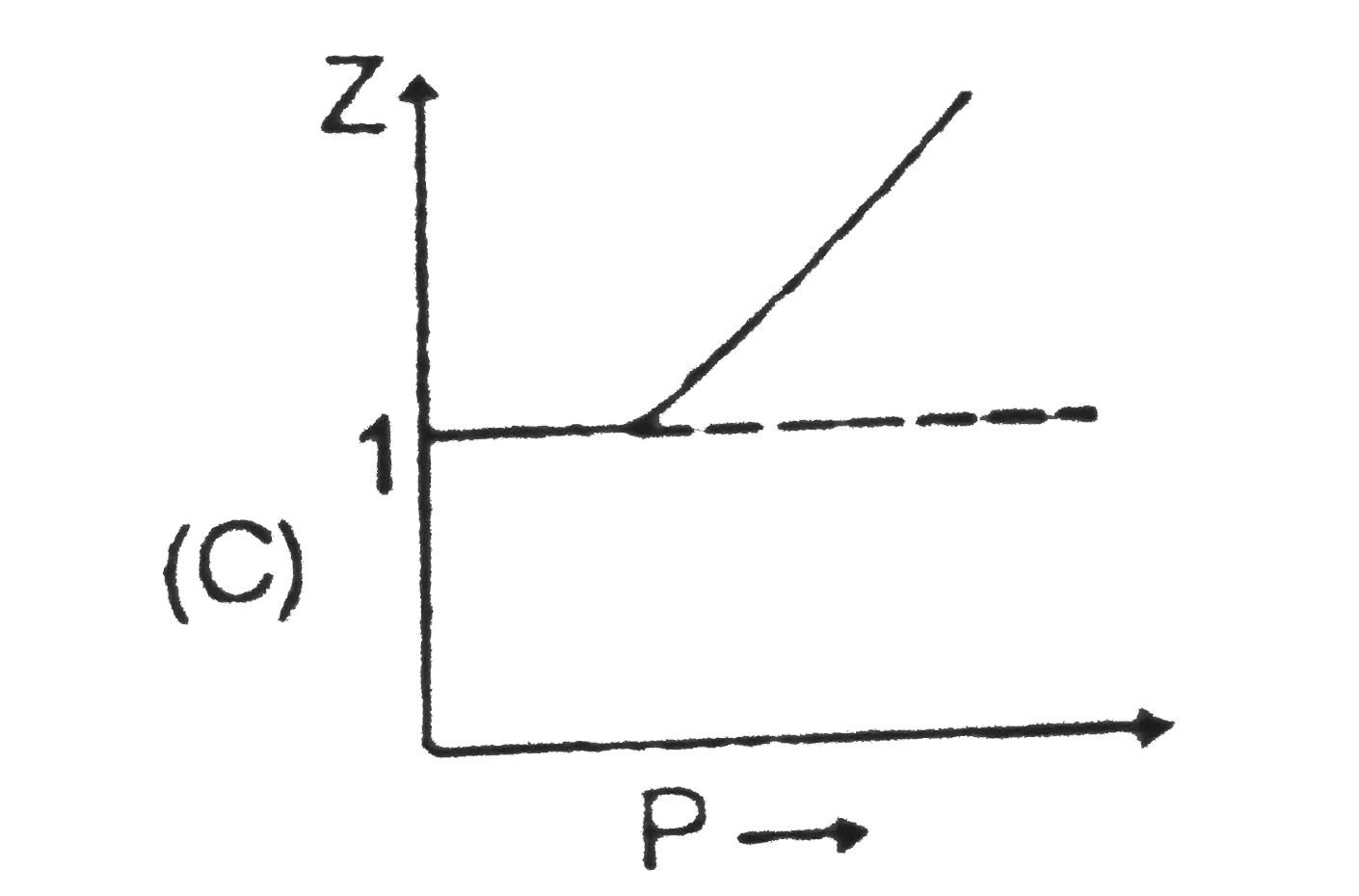
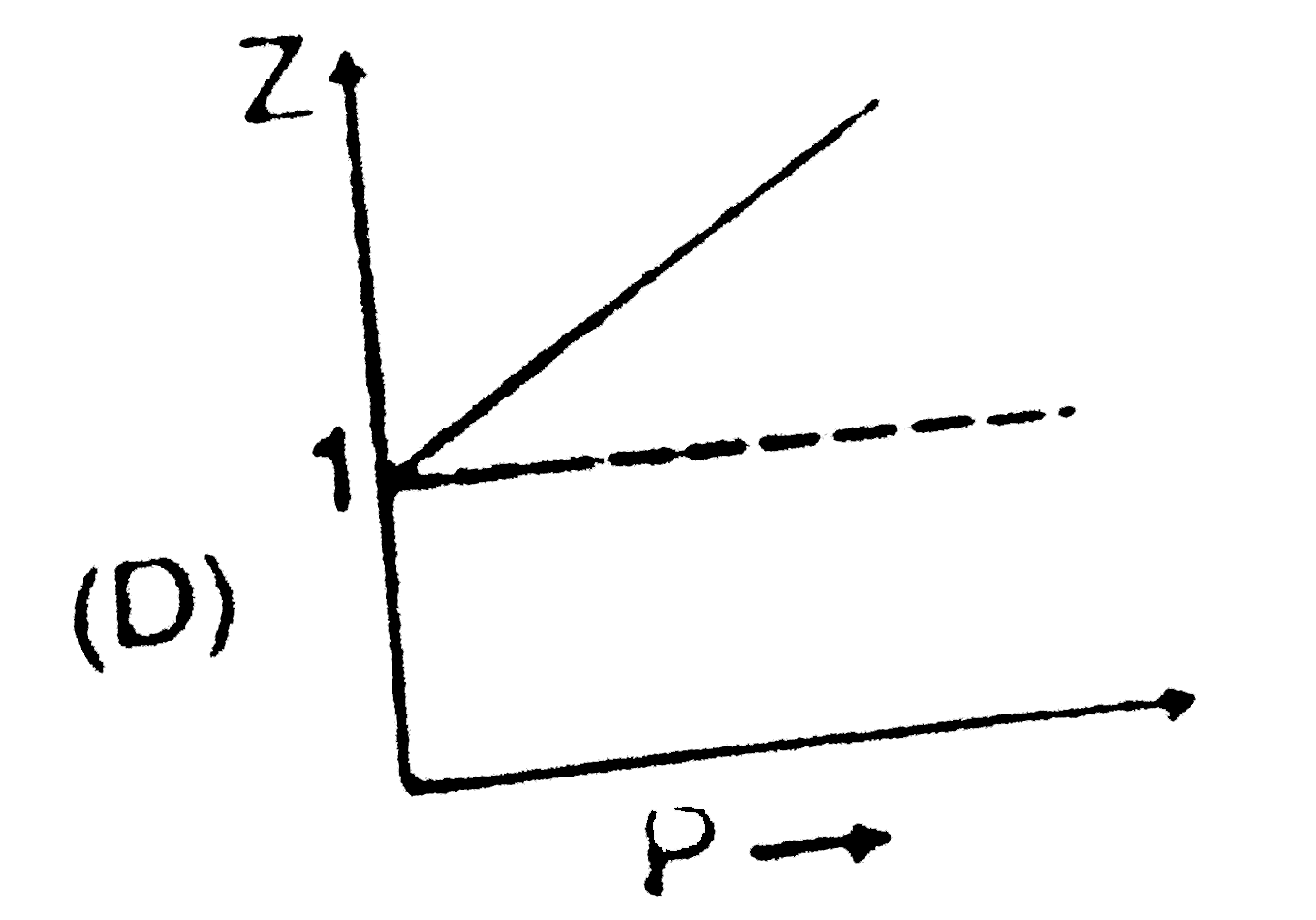A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
RESONANCE ENGLISH-RANK BOOSTER-All Questions
- Sketch shows the plot of Z v/s P for a hypothetical gas for one mole a...
Text Solution
|
- At 200 K and 500 atm value of compressibility factor is 2.Then volume ...
Text Solution
|
- At high pressure suppose all the constant temperature curve varies lin...
Text Solution
|
- Sketch shows the plot of Z v/s P for a hypothetical gas for one mole a...
Text Solution
|
- Match List : {:("Column-I","Column-II"),((A)PV^(gamma)="Constant",(p...
Text Solution
|
- The number of moles present in 54.5 g of HSO is
Text Solution
|
- The number of moles present in 84 g of HSO is
Text Solution
|
- How many moles are represented by 130 g of glucose,
Text Solution
|
- How many moles are represented by 150 g of glucose
Text Solution
|
- How many moles are represented by 120 g of glucose
Text Solution
|
- Consider the following figure at 500 K.Assuming ideal gas behaviour, c...
Text Solution
|
- If above tube is placed vertically with the open and upward then find ...
Text Solution
|
- In a tyre of "Ferrari" car of Mr. Obama, a tube having a volume of 12....
Text Solution
|
- 2 moles of Ne gas and 5 moles of He gas, both samples having average v...
Text Solution
|
- Two glass bulbs of equal volume are connected by a narrow tube and are...
Text Solution
|
- According to Maxwell's distribution of molecular speeds, the following...
Text Solution
|
- A bulb of constant volume is attached to a manometer tube open at othe...
Text Solution
|
- The pressure exerted by 12 g of an ideal gas at temperature T^(@)C in...
Text Solution
|
- A 4: 1 molar mixture of He and CH4 is contained in a vessel at 20 bar ...
Text Solution
|
- What mass of potassium chlorate (KClO3) on heating gives 1.691 g of po...
Text Solution
|