Home
Class 12
PHYSICS
A wave pulse moving along the x axis is ...

A wave pulse moving along the `x` axis is represented by the wave funcation
`y(x, t) = (2)/((x - 3t)^(2) + 1)`
where `x` and `y` are measured in `cm` and `t` is in seconds.
`(i)` in which direction is the wave moving ?
`(ii)` Find speed of the wave.
`(iii)` Plot the waveform at `t = 0, t = 2s`.

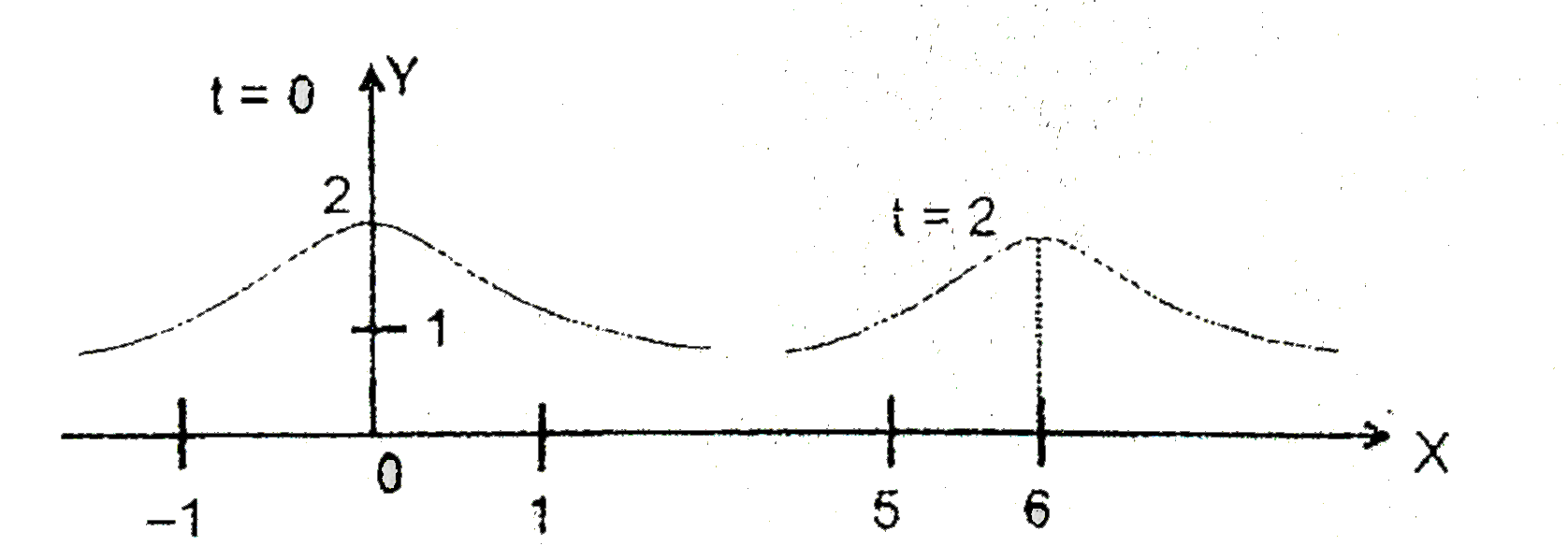
Text Solution

Verified by Experts

The correct Answer is:
(i) Positive `xa` , (ii) `3 cm//s`.
`y = (2)/((x-3t)^(2) + 1)`
`(i)` As wave is moving in `+ve x` direction because
`y = (x, t) = f(t - x//AA) = f//v(vt - x)`
`(ii)` Now `x - vt` is concerened with `x - 3t`
`:. V = 3 cm//sec`.
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • WAVE ON STRING

    RESONANCE ENGLISH|Exercise Board Level Exercise|27 Videos

  • WAVE ON STRING

    RESONANCE ENGLISH|Exercise Exercise- 1 PART I|23 Videos

  • WAVE ON STRING

    RESONANCE ENGLISH|Exercise Exercise- 3 PART II|7 Videos

  • TRAVELLING WAVES

    RESONANCE ENGLISH|Exercise Exercise- 3 PART I|19 Videos

  • WAVE OPTICS

    RESONANCE ENGLISH|Exercise Advanced Level Problems|8 Videos

Similar Questions

Explore conceptually related problems

A pulse moving to the right along the x-axis is represented by the wave function where x and y are measured in cedntimetres and t is measured in seconds. Find expression for the wave function at t=0, t=1.0 s, and t=2.0 s and plote the shape of pulse at these lines.

The wave function of a pulse is given by y= (3)/((2x+3t)^(2)) where x and y are in metre and t is in second (i) Identify the direction of propagation. (ii) Determine the wave velocity of the pulse.

The wave function of a pulse is given by y=(5)/((4x+6t)^(2)) where x and y are in metre and t is in second :- (i) Identify the direction of propagation (ii) Determine the wave velocity of the pulse

A wave pulse on a horizontal string is represented by the function y(x, t) = (5.0)/(1.0 + (x - 2t)^(2)) (CGS units) plot this function at t = 0 , 2.5 and 5.0 s .

A tavelling harmonic wave is represented by the equation y(x,t)=10^(-3) sin (50t+2x), where x and Y are in meter and t is in seconds . Which of the following is a correct statement about the wave?

y(x, t) = 0.8//[4x + 5t)^(2) + 5] represents a moving pulse, where x and y are in meter and t in second. Then

The equation of a wave is y=4 sin[(pi)/(2)(2t+(1)/(8)x)] where y and x are in centimeres and t is in seconds.

A wave is represented by the equation : y = A sin(10 pi x + 15 pi t + pi//3) where, x is in metre and t is in second. The expression represents.

A travelling wave pulse is given by y = (10)/(5 + (x + 2t)^(2)) Here, x and y are in meter and t in second. In which direction and with what velocity is the pulse propagation. What is the ampitude of pulse?

The equation of a wave id represented as Y=2sin(Πx - 200Πt) where x and y are in cm and t is in second. The wave velocity is

Home
Profile