Home
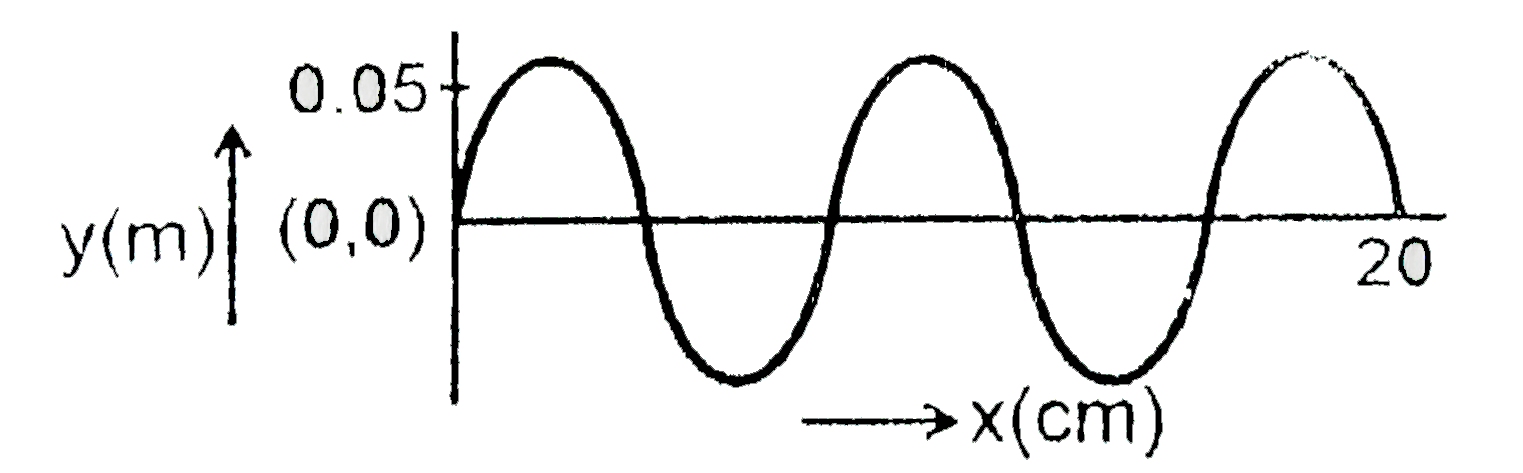
Class 12
PHYSICS
For the wave shown in figure, the equati...

For the wave shown in figure, the equation for the wave, travelling along `+x` acis with velocity `350 ms^(-1)` when its position at `t = 0` is as shown

A

`0.05 sin ((314)/(4)x - 27475 t)`

B

`0.05 sin ((379)/(5)x - 27475 t)`

C

`1 sin ((314)/(4)x - 27475 t)`

D

`0.05 sin ((289)/(5)x + 27475 t)`

Text Solution

Verified by Experts

The correct Answer is:
A
Promotional Banner

Topper's Solved these Questions

  • WAVE ON STRING

    RESONANCE ENGLISH|Exercise Exercise- 2 PART I|21 Videos

  • WAVE ON STRING

    RESONANCE ENGLISH|Exercise Exercise- 2 PART II|19 Videos

  • WAVE ON STRING

    RESONANCE ENGLISH|Exercise Exercise- 1 PART I|23 Videos

  • TRAVELLING WAVES

    RESONANCE ENGLISH|Exercise Exercise- 3 PART I|19 Videos

  • WAVE OPTICS

    RESONANCE ENGLISH|Exercise Advanced Level Problems|8 Videos

Similar Questions

Explore conceptually related problems

For the wave shown in figure, write the equation of this wave if its position is shown at t= 0 . Speed of wave is v = 300m//s .

the equation of a wave travelling along the positive x - axis ,as shown in figure at t = 0 is given by

The equation of a wave travelling along the positive x-axis, as shown in figure at t = 0 is given by

In the figure shown the block B moves with , velocity 10 ms^(-1) . The velocity of A in the position shown is

in a sine wave ,postive of different particles at time t=0 is shown in figure. The equation for this wave if it is travelling along postive x -axis can beB

y-x curve at an instant for a wave travelling along x- axis on a string is shown. Slope at the point A on the curve, as shown, is tan 53^(@) .

y-x curve at an instant for a wave travelling along x- axis on a string is shown. Slope at the point A on the curve, as shown, is tan 53^(@) .

The equation of a transverse wave travelling along +x axis is given by y=0.15 sin (1.57x-31.4t) where y and x are represented in m and t in s. Find the amplitude, frequency velocity and wavelength of the wave.

The graph shows a wave at t=0 travelling to the right with a velocity of 4 m//s . The equation that best represents the wave is

A transverse harmonic wave of amplitude 0.01 m is genrated at one end (x=0) of a long horizontal string by a tuning fork of frequency 500 Hz. At a given instant of time the displacement of the particle at x=0.1 m is -0.005 m and that of the particle at x=0.2 m is +0.005 m. calculate the wavelength and the wave velocity. obtain the equetion of the wave assuming that the wave is traveling along the + x-direction and that the end x=0 is at he equilibrium position at t=0.

RESONANCE ENGLISH-WAVE ON STRING -Exercise- 1 PART II
  1. For the wave shown in figure, the equation for the wave, travelling al...

    Text Solution

    |

  2. The displacement of a wave disturbance propagating in the positive x-d...

    Text Solution

    |

  3. A travelling wave is described by the equation y = y(0) sin2 pi ((ft -...

    Text Solution

    |

  4. A travelling wave on a string is given by y = A sin [alphax + betat + ...

    Text Solution

    |

  5. A transverse wave of amplitude 0.5 m and wavelength 1 m and frequency ...

    Text Solution

    |

  6. Two small boats are 10m apart on a lake. Each pops up and down with a ...

    Text Solution

    |

  7. A wave pulse is generated in a string that lies along x- axis. At the ...

    Text Solution

    |

  8. Wave pulse on a string shown in figure is moving to the right without ...

    Text Solution

    |

  9. An observer standing at the sea coast observes 54 waves reaching the c...

    Text Solution

    |

  10. Both the strings, shown in figure, are made of same material and have ...

    Text Solution

    |

  11. Three blocks I, II, & III having mass of 1.6 kg, 1.6 kg and 3.2 kg rep...

    Text Solution

    |

  12. Three consecutive flash photographs of a travelling wave on a string w...

    Text Solution

    |

  13. A heavy ball is suspended from the ceiling of a motor car through a li...

    Text Solution

    |

  14. A wave moving with constant speed on a uniform string passes the point...

    Text Solution

    |

  15. A particle of mass m executing SHM with amplitude A and angular freque...

    Text Solution

    |

  16. Sinusoidal waves 5.00 cm in amplitude are to be transmitted along a st...

    Text Solution

    |

  17. The average power transmitted through a given point on a string suppor...

    Text Solution

    |

  18. Two waves of same amplitude a and frequency v and having a phase diffe...

    Text Solution

    |

  19. The rate of transfer of energy in a wave depends

    Text Solution

    |

  20. Two waves of equal amplitude A, and equal frequency travel in the same...

    Text Solution

    |