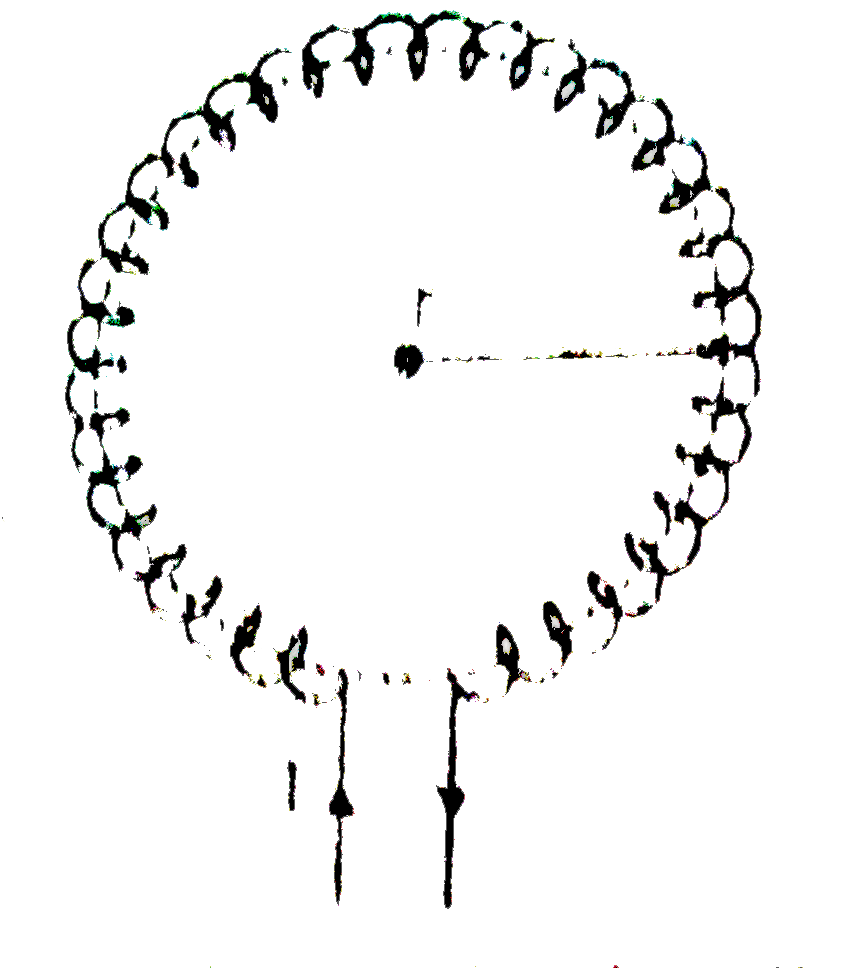Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
RESONANCE ENGLISH-ELECTRODYNAMICS-Exercise-3 PART-3
- Define magnetic susceptibility of a material. Name two elements, one...
Text Solution
|
- Magnetic field liness can be entirely confined within the core of a to...
Text Solution
|
- An electron does not suffer any deflection while passing through a reg...
Text Solution
|
- Write the expression for the magnetic moment (m) due to a planar squar...
Text Solution
|
- A long straight wire, of circular cross section (radius =a) carries a ...
Text Solution
|
- A beam of alpha particles projected along +x- axis , experiences a fo...
Text Solution
|
- Deduce an expression for the magnetic dipole moment of an electron orb...
Text Solution
|
- The permeability of magnetic material is 0.9983. Name the type of magn...
Text Solution
|
- A magnetic needle free to rotate in a vertical plane parallel to the m...
Text Solution
|
- (a)Using Ampere's circuital law, obtain the expression for the magneti...
Text Solution
|
- (a) Write the expression for the force, vecF, acting on a charged part...
Text Solution
|
- What are permanent magnets? Give one example.
Text Solution
|
- A proton and a deuteron having equal momenta enter in a a region of a ...
Text Solution
|
- In given diagrams write the direction of magnetic field produced at po...
Text Solution
|
- Write Biot-Savart law. Write the path of motion of an electron when i...
Text Solution
|
- A long straight wire of a circular cross section (radius a) carrying s...
Text Solution
|
- Using the concept of force between two infinitely long parallel curren...
Text Solution
|
- Show diagrammatically the behaviour of magnetic field lines in the pre...
Text Solution
|
- If magnetic monpole existed, how would Gauss law of magnetism be modif...
Text Solution
|
- Derive the expression for force per unit length between two long strai...
Text Solution
|