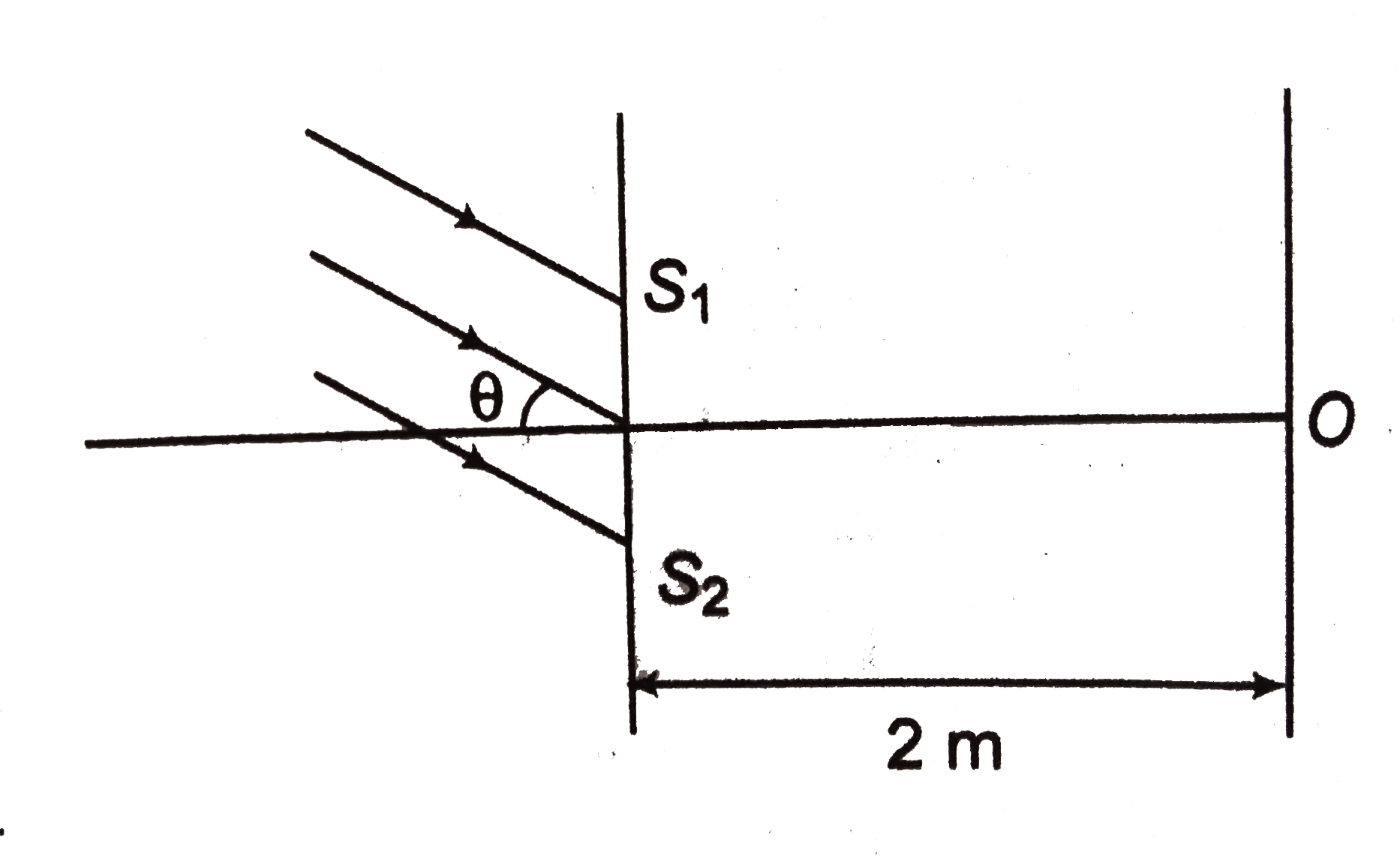
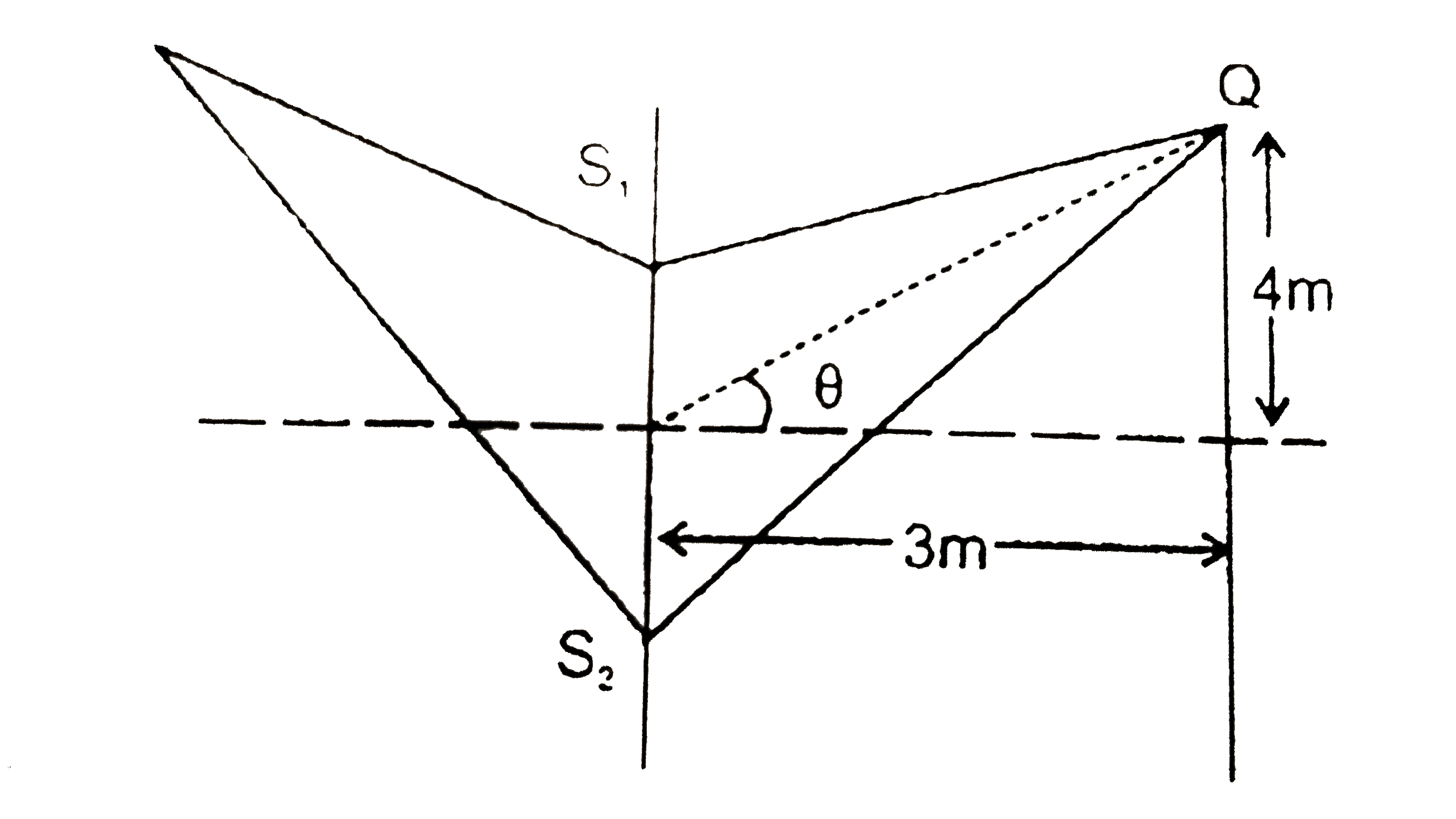
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
RESONANCE ENGLISH-WAVE OPTICS-Exercise-2 (Part-3)
- In Young's double slit experiment the ratio of intensitities of bright...
Text Solution
|
- A parallel beam of light (lambda= 5000 Å) is incident at an angle thet...
Text Solution
|
- A Young's double slit experiment is performed with white light.
Text Solution
|
- In an interference arrangement similar to Young's double-slit experime...
Text Solution
|
- In Young's double slit experiment, white light is used. The separation...
Text Solution
|