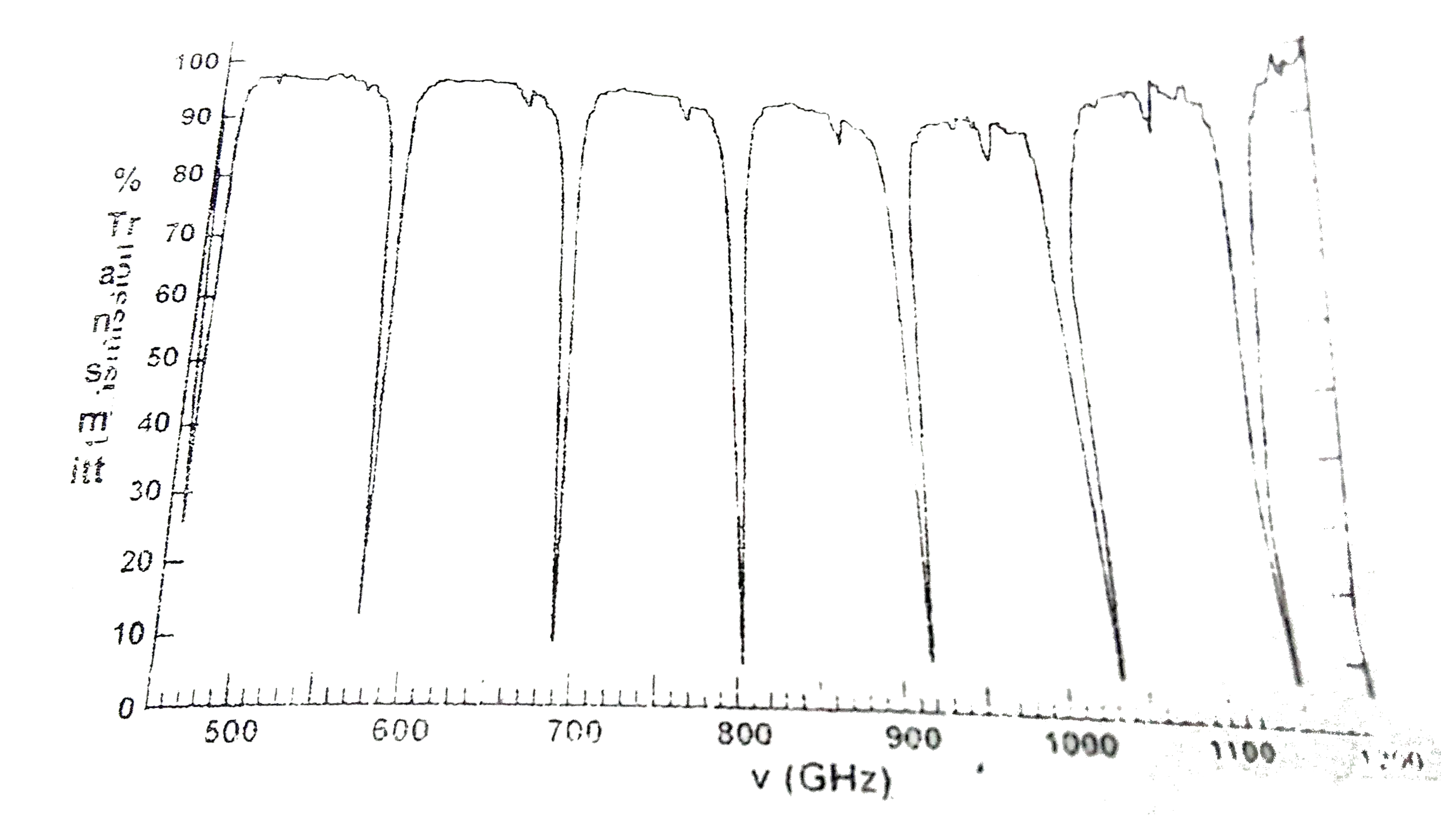
Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
- Rotational energy levels of diatomic molecules are well described by t...
Text Solution
|
- For an HCI molecule find the rotational quantum numbers of two neighbo...
Text Solution
|
- Find the number of ratational levels per unit energy interval, dN//dE,...
Text Solution
|
- In a diatomic molecule, the rotational energy at given temperature
Text Solution
|
- A(2) and B(2) are two diatomic molecules with bond energies of A-A and...
Text Solution
|
- Rotational energy levels of diatomic molecules are well described by t...
Text Solution
|
- The energy absorbed by each molecule (A(2)) of a substance is 4.4 xx 1...
Text Solution
|
- एक पदार्थ के प्रत्येक अणु (A(2)) द्वारा अवशोषित ऊर्जा 4.4 xx 10^(-1...
Text Solution
|
- The energy required to rotate ethane molecule about the carbon ...
Text Solution
|