Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
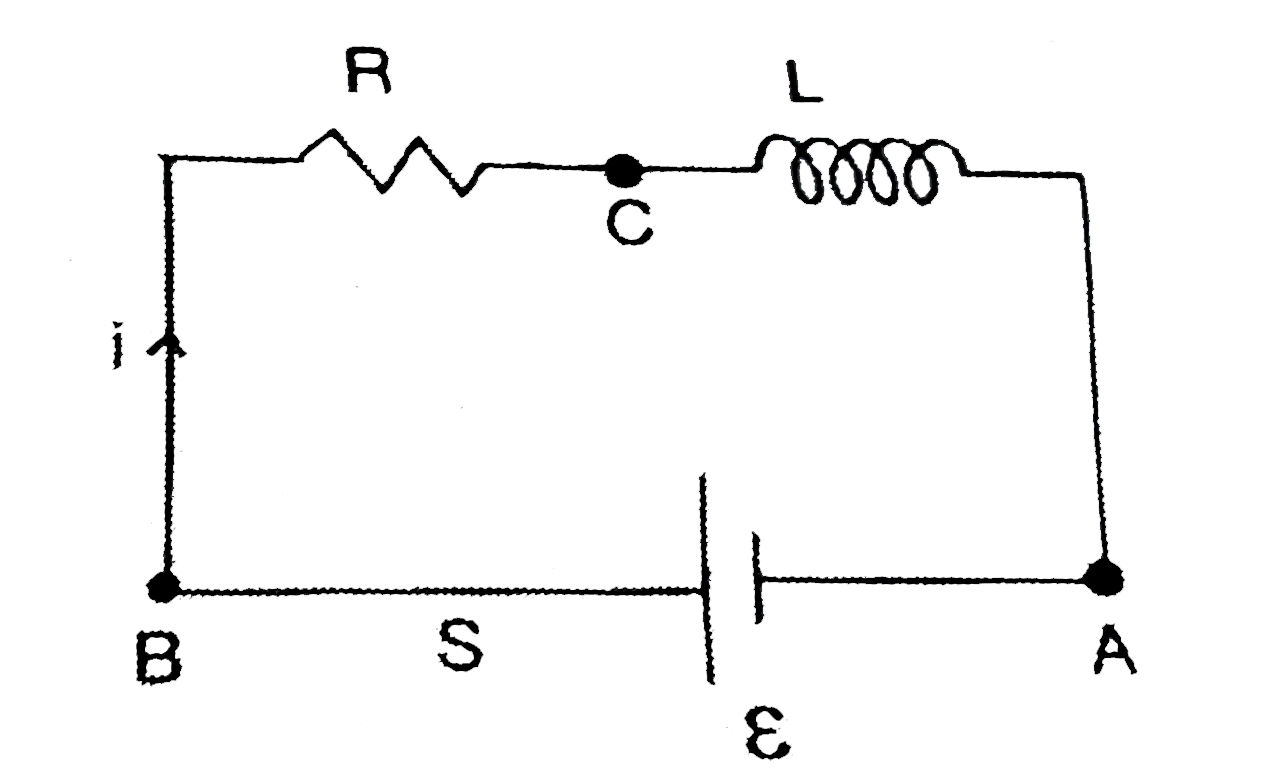
- Figure shows a circuit consisting of a ideal cell, an inductor L and a...
Text Solution
|
- The switch in figure is closed at time t = 0 . Find the current in the...
Text Solution
|
- In the circuit shown, switch S is closed at time t = 0 . Find the curr...
Text Solution
|
- In the following circuit (Fig.)the switch is closed at t = 0. Intially...
Text Solution
|
- Figure shows a circuit consisting of an ideal cell, an inductor L , an...
Text Solution
|
- A circuit contains an ideal cell and an inductor with a switch. Initia...
Text Solution
|
- Consider a circuit consists of resistors, inductor, battery and a swit...
Text Solution
|
- At t=0 , switch S is closed. Find time constant of the circuit and cur...
Text Solution
|
- Consider a L-R circuit shown in figure. There is no current in circuit...
Text Solution
|