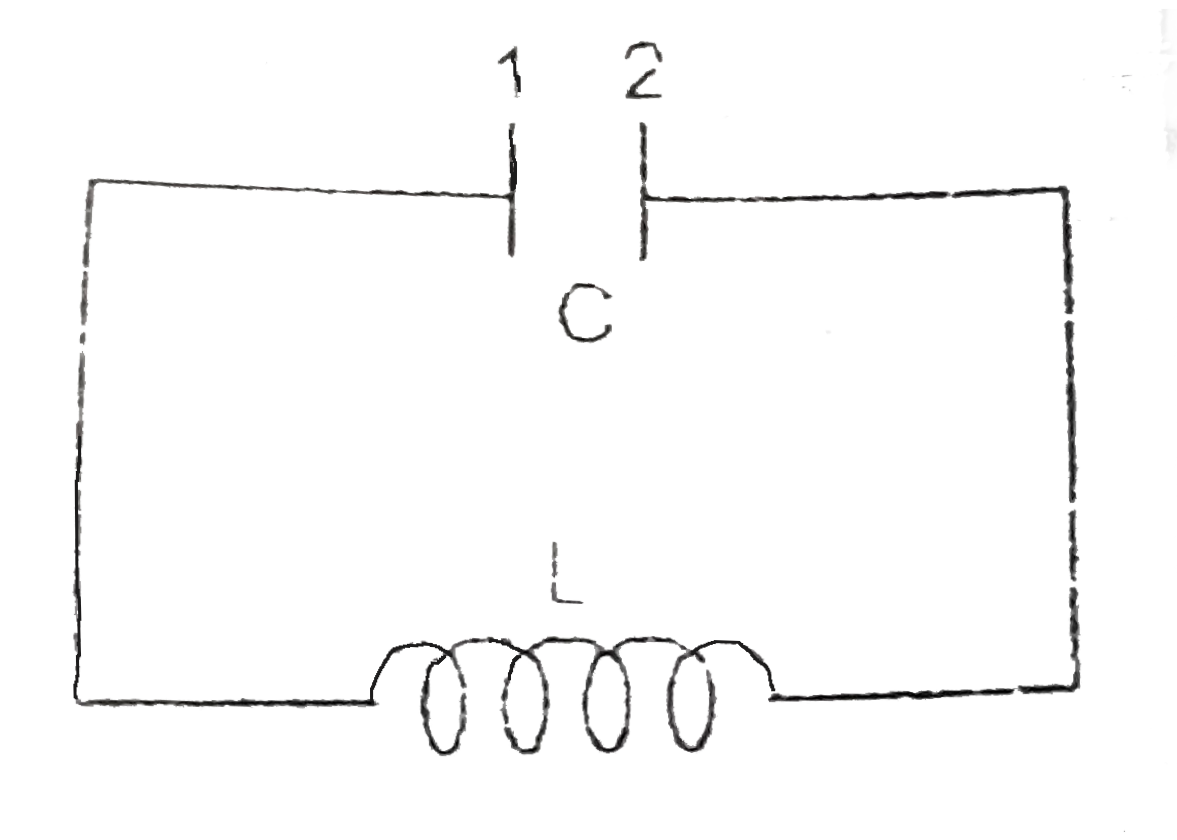
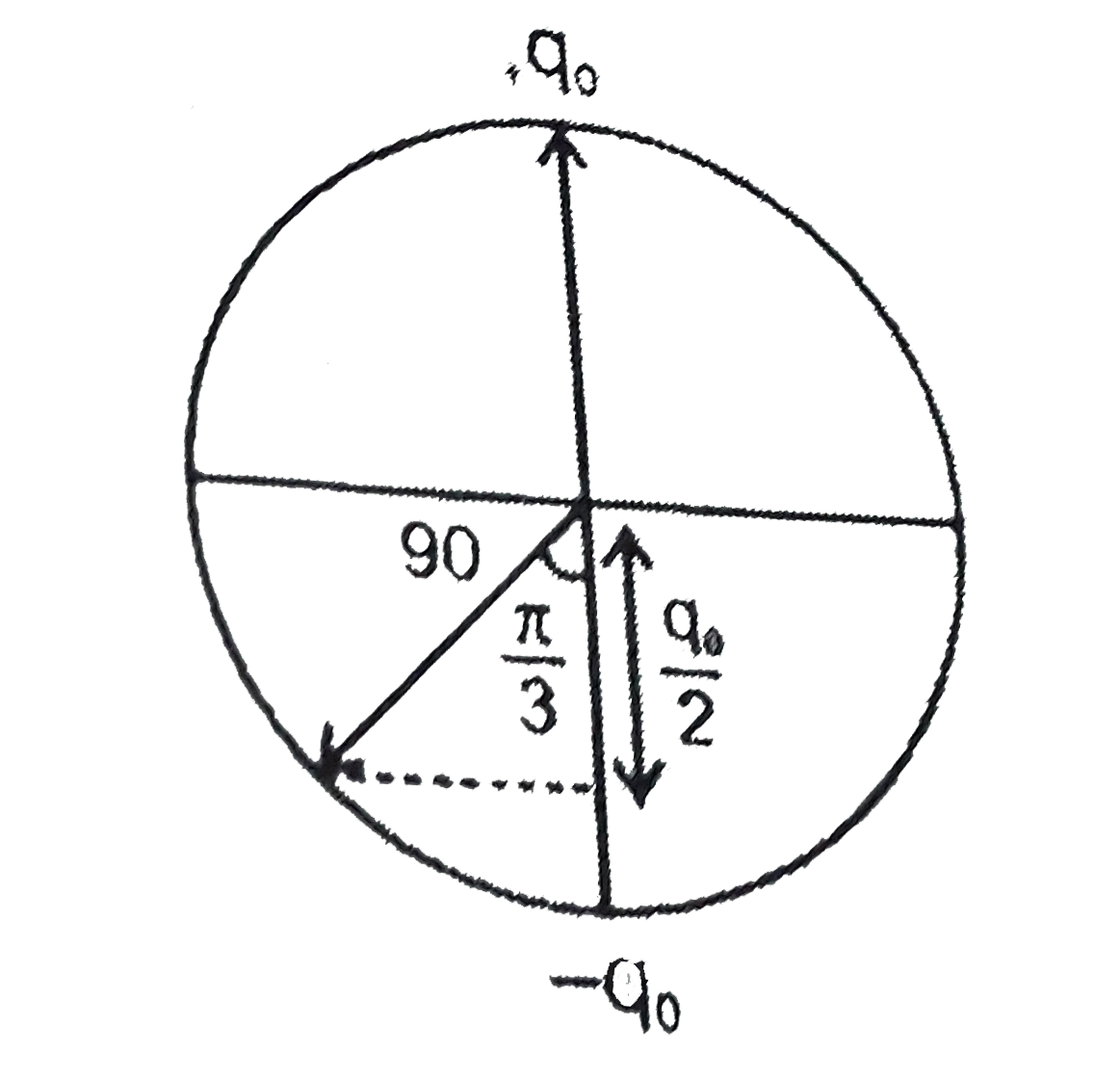
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Consider a L-C oscillation circuit. Circuit elements has zero resistan...
Text Solution
|
- The radioactivity of a sample is R(1) at a time T(1) and R(2) at time ...
Text Solution
|
- The radioactivity of a sample is R(1) at a time T(1) and R(2) at a ti...
Text Solution
|
- A coil having inductance and L and resistance R is connected to a batt...
Text Solution
|
- Consider a L-C oscillation circuit. Circuit elements has zero resistan...
Text Solution
|
- चित्र 2.5-2में प्रदर्शित L-C परिपथ के संधारित्र पर प्रारम्भिक आवेश 1...
Text Solution
|
- In an LC circuit, resistance of the circuit is negligible. If time per...
Text Solution
|
- In an LC circuit, resistance of the circuit is negligible. If time per...
Text Solution
|
- ஒரு மின்சுற்றுக் கோட்பாட்டின்படி, C(t) என்ற நேரிய சுற்று, C(at(1) + bt...
Text Solution
|