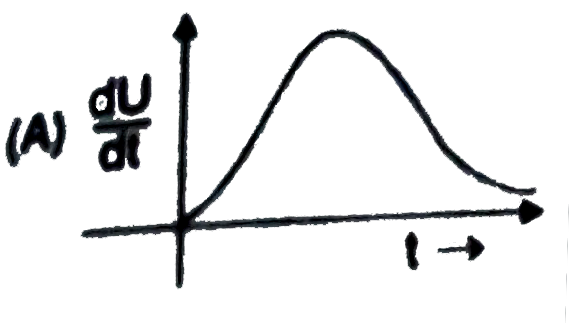
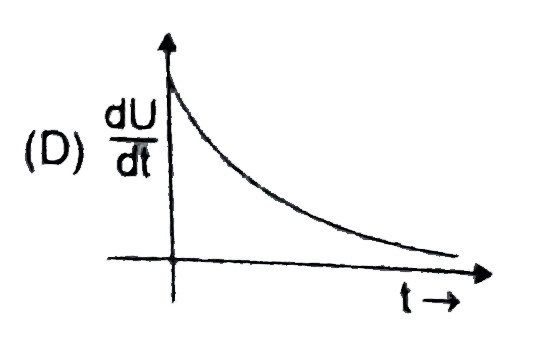
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Rate of increment of energy in an inductor with time in series RL circ...
Text Solution
|
- An inductor-resistance -battery circuit is switched on at t = 0. If th...
Text Solution
|
- In an LR circuit connected to a battery, the rate at which energy is s...
Text Solution
|
- A inductor of 20mH inductance and a resistor of 100 Omega resistance a...
Text Solution
|
- Rate of increment of energy in an inductor with time in series RL circ...
Text Solution
|
- The figure below shows a battery of emf epsilon connected to an induct...
Text Solution
|
- As shown in the figure, a battery of emf is connected to an inductor L...
Text Solution
|
- Self inductance| Inductors and RL circuits
Text Solution
|
- Questions based on Self inductance| Inductors and RL circuits
Text Solution
|