Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
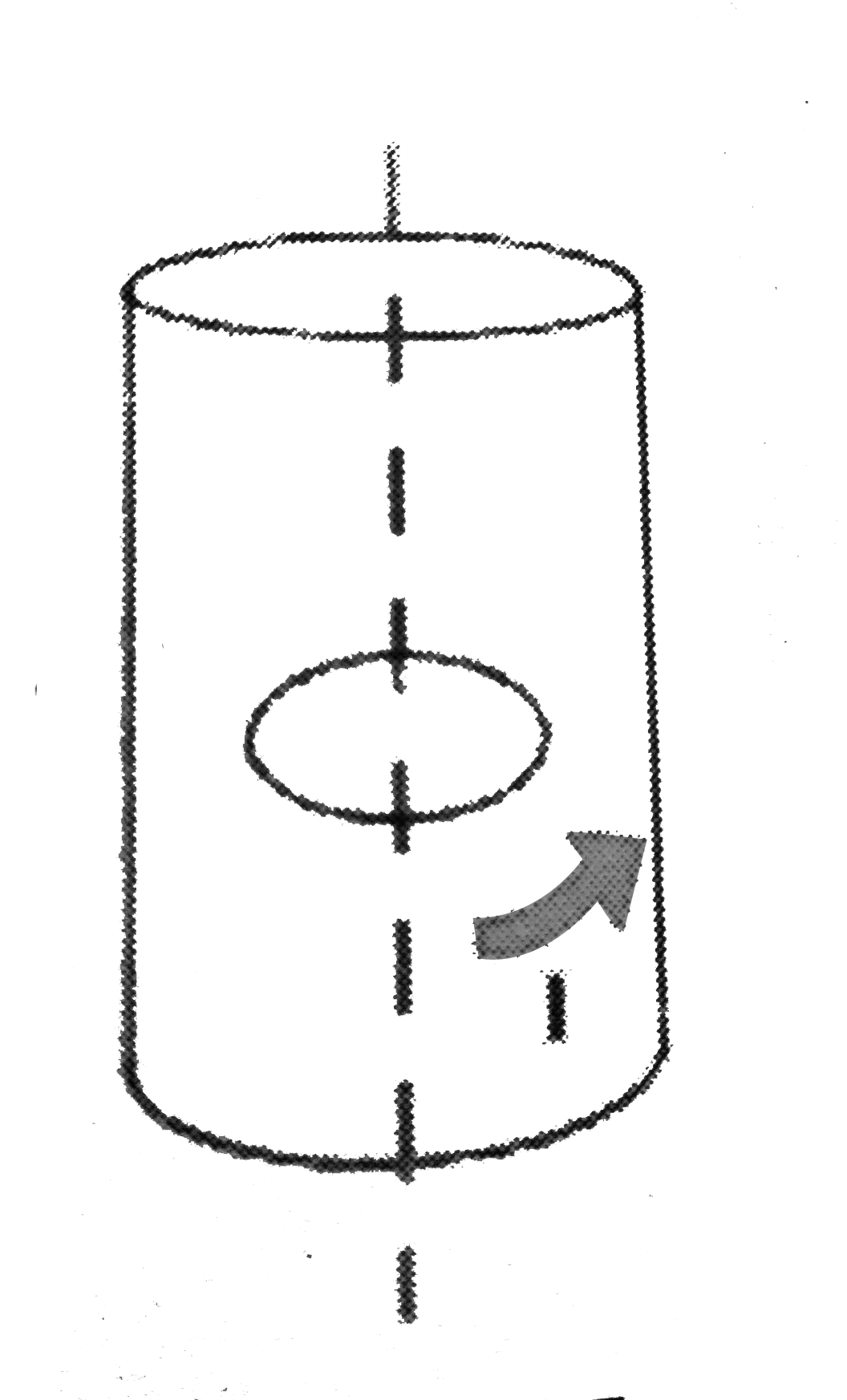
- A long circular tube of length 10 m and radius 0.3 m carries a current...
Text Solution
|
- A thin but long, hollow, cylindrical tube of radius r carries a curre...
Text Solution
|
- A long circular tube of length 10 m and radius 0.3 m carries a current...
Text Solution
|
- In Fig. there is a conducting loop ABCDEF of resistance lambda per uni...
Text Solution
|
- In Fig. there is a conducting loop ABCDEF of resistance lambda per uni...
Text Solution
|
- In Fig. there is a conducting loop ABCDEF of resistance lambda per uni...
Text Solution
|
- A long copper tube of inner radius R carriers a current i. The magneti...
Text Solution
|
- A straight wire carrying a current is turned into a circular loop ...
Text Solution
|
- 10 मी लम्बी गोल ट्यूब, जिसकी त्रिज्या 0.3 मी है, के वक्रीय-पृष्ठ में। ...
Text Solution
|