Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- In the figure shown a conducting rod of length l resistance R & mass m...
Text Solution
|
- Figure shows a conducting rod of negligible resistance that can slide ...
Text Solution
|
- Figure shows a conducting rod of length l = 10 cm , resistance R and m...
Text Solution
|
- AB and CD are fixed conducting smooth rails placed in a vertical palne...
Text Solution
|
- In the shown figure, there are two long fixed parallel conducting rail...
Text Solution
|
- In the shown figure, there are two long fixed parallel conducting rail...
Text Solution
|
- In the shown figure, there are two long fixed parallel conducting rail...
Text Solution
|
- A conducting rod PQ of mass m and length l is placed on two long paral...
Text Solution
|
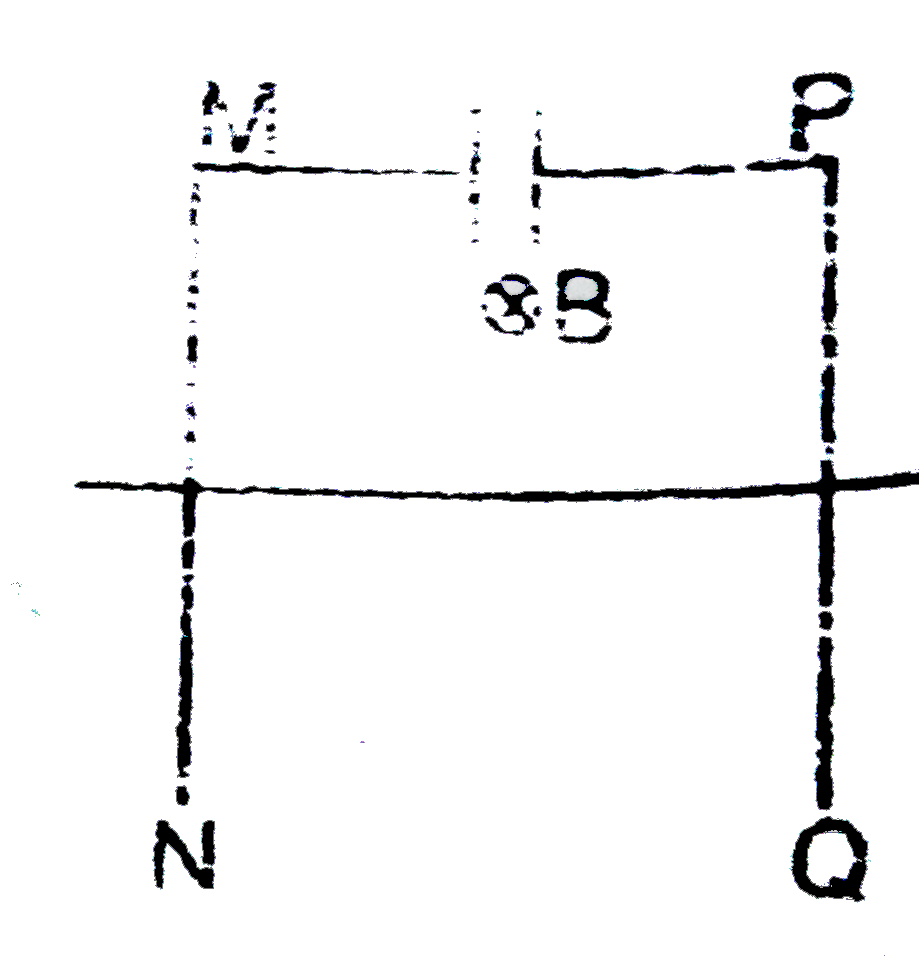
- A conducting rod MN of mass m and length 'l' is placed on parallel smo...
Text Solution
|