Home
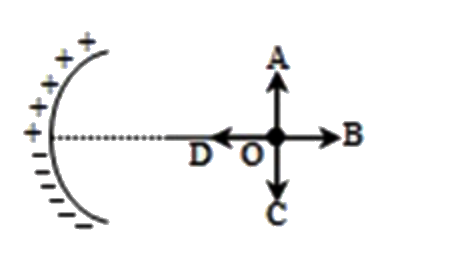
Class 12
PHYSICS
The linear charge density on upper half ...

The linear charge density on upper half of segment of ring is `lamda` and at lower half it is `-lamda` . The direction of electric field at centre O of ring is

A

along OA

B

along OB

C

along OC

D

along OD

Text Solution

Verified by Experts

The correct Answer is:
C
Promotional Banner

Topper's Solved these Questions

  • ELECTROSTATICS

    RESONANCE ENGLISH|Exercise Part - II Section (C)|14 Videos

  • ELECTROSTATICS

    RESONANCE ENGLISH|Exercise Part - II Section (D)|2 Videos

  • ELECTROSTATICS

    RESONANCE ENGLISH|Exercise Part - II Section (A)|4 Videos

  • ELECTROMAGNETIC INDUCTION

    RESONANCE ENGLISH|Exercise A.l.P|19 Videos

  • EXPERIMENTAL PHYSICS

    RESONANCE ENGLISH|Exercise PART -II|10 Videos

Similar Questions

Explore conceptually related problems

The linear charge density on upper half of semi-circular section of ring is lambda and that at lower half is -lambda . The direction of electric field at centre O of ring is :

The charge per unit length of the four quadrant of the ring is 2 lambda, -2lambda, lambda and -lambda respectively. The electric field at the centre is:

A half ring of radius r has a linear charge density lambda .The potential at the centre of the half ring is

Charge q is uniformly distributed over a thin half ring of radius R . The electric field at the centre of the ring is

Two semicircular rings lying in same plane, of uniform linear charge density lambda have radius r and 2r. They are joined using two straight uniformly charged wires of linear charge density lambda and length r as shown in figure. The magnitude of electric field at common centre of semi circular rings is -

Two semicircular rings lying in same plane, of uniform linear charge density lambda have radius r and 2r. They are joined using two straight uniformly charged wires of linear charge density lambda and length r as shown in figure. The magnitude of electric field at common centre of semi circular rings is -

Find the electric field at centre of semicircular ring shown in figure . .

A small part of dl length is removed from a ring having charge per unit length lamda . Find electric field at centre due to remaining ring.

The linear charge density on a ring of radius R is lambda=lambda_0 sin (theta) where lambda_0 is a constant and theta is angle of radius vector of any point on the ring with x-axis. The electric potential at centre of ring is

If the resistance of the upper half of rigid loop is twice that of the lower half, the magnitude of magnetic induction at the centre is equal to