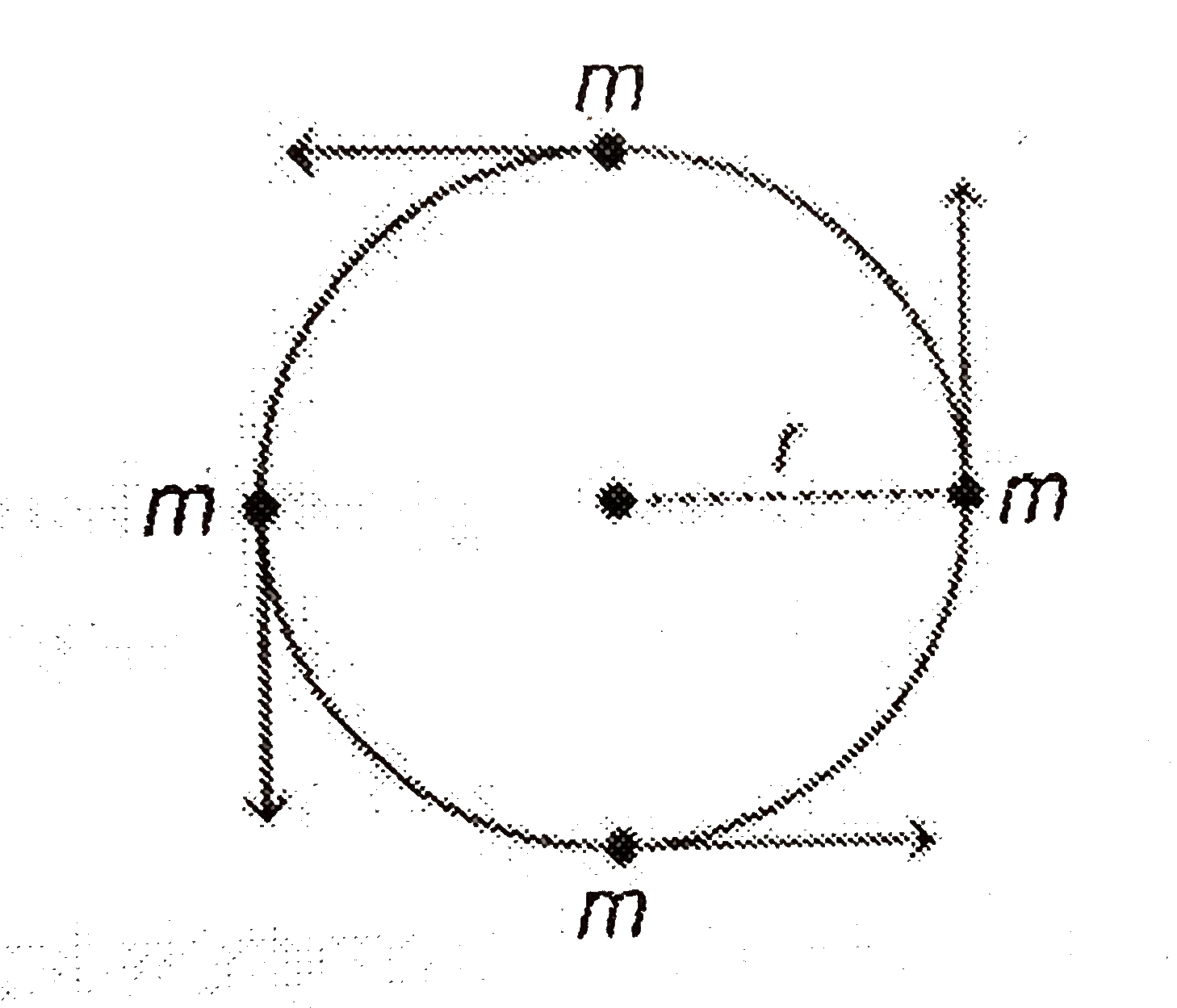Home
Class 12
PHYSICS
Four similar particles of mass m are orb...

Four similar particles of mass m are orbiting in a circle of radius r in the same direction and same speed because of their mutual gravitational attractive force as shown in the figure . Speed of a particle is given by

A

`[(Gm)/(r)((1+2sqrt2)/(4))]^(1/(2))`

B

`root(3)((GM)/(r))`

C

`sqrt((Gm)/(r)(1+2sqrt2))`

D

zero

Text Solution

Verified by Experts

The correct Answer is:
A
Promotional Banner

Topper's Solved these Questions

  • GRAVITATION

    RESONANCE ENGLISH|Exercise EXERCISE-1 PART-3|2 Videos

  • GRAVITATION

    RESONANCE ENGLISH|Exercise EXERCISE-2 PART-1|15 Videos

  • GRAVITATION

    RESONANCE ENGLISH|Exercise EXERCISE-1 PART-1|9 Videos

  • GEOMATRICAL OPTICS

    RESONANCE ENGLISH|Exercise Advance level Problems|35 Videos

  • NUCLEAR PHYSICS

    RESONANCE ENGLISH|Exercise Advanced level solutions|16 Videos

Similar Questions

Explore conceptually related problems

Two particles of equal mass (m) each move in a circle of radius (r) under the action of their mutual gravitational attraction find the speed of each particle.

Two particles of equal mass go round a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.

Two particles of equal mass go around a circle of radius R under the action of their mutual gravitational attraction. The speed v of each particle is

Four particles of equal masses M move along a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.

Four particles of equal mass are moving round a circle of radius r due to their mutual gravitational attraction . Find the angular velocity of each particle .

Four particles, each of mass M and equidistant from each other, move along a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is:

Four particles, each of mass M and equidistant from each other, move along a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is:

Four particles, each of mass M and equidistant from each other, move along a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is:

Three particles of equal mass M each are moving on a circular path with radius r under their mutual gravitational attraction. The speed of each particle is

Two particles of equal masses m go round a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is v=sqrt((Gm)/(nR)) . Find the value of n.

RESONANCE ENGLISH-GRAVITATION-EXERCISE-1 PART-2
  1. Four similar particles of mass m are orbiting in a circle of radius r ...

    Text Solution

    |

  2. Two blocks of masses m each are hung from a balances as shown in the f...

    Text Solution

    |

  3. Three particales P,Q and R are placedd as per given Masses of P,Q and ...

    Text Solution

    |

  4. Three particle each of mass m, are located at the vertices of an equil...

    Text Solution

    |

  5. Let gravitation field in a space be given as E = - (k//r) If the refer...

    Text Solution

    |

  6. Gravitational field intensity at the centre of the semi circle formed ...

    Text Solution

    |

  7. Infinite number of bodies, each of mass 2kg are situated on X-axis at ...

    Text Solution

    |

  8. Two concentric shells of uniform density of mass M(1) and M(2) are sit...

    Text Solution

    |

  9. Figure show a hemispherical shell having uniform mass density The dire...

    Text Solution

    |

  10. Mass M is uniformly distributed only on curved surface of a thin hemis...

    Text Solution

    |

  11. A body starts from rest from a point distant r(0) from the centre of t...

    Text Solution

    |

  12. Three equal masses each of mass 'm' are placed at the three-corner of ...

    Text Solution

    |

  13. Three equal masses each of mass 'm' are placed at the three-corner of ...

    Text Solution

    |

  14. Three identical particles each of mass M are placed at the corners of ...

    Text Solution

    |

  15. Three equal masses each of mass 'm' are placed at the three-corner of ...

    Text Solution

    |

  16. A satellite is revolving round the earth in circular orbit

    Text Solution

    |

  17. An artificial satellite of the earth releases a packet. If air resista...

    Text Solution

    |

  18. Figure shows the variation of energy E with the orbit radius r of a sa...

    Text Solution

    |

  19. A planet of mass m moves around the sun of mass M in an elliptical orb...

    Text Solution

    |

  20. The escape velocity from the earth is 11.2km//s. If a body is to be pr...

    Text Solution

    |