A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
GRAVITATION
RESONANCE ENGLISH|Exercise EXERCISE-2 PART-2|10 VideosGRAVITATION
RESONANCE ENGLISH|Exercise EXERCISE-2 PART-3|12 VideosGRAVITATION
RESONANCE ENGLISH|Exercise EXERCISE-1 PART-3|2 VideosGEOMATRICAL OPTICS
RESONANCE ENGLISH|Exercise Advance level Problems|35 VideosNUCLEAR PHYSICS
RESONANCE ENGLISH|Exercise Advanced level solutions|16 Videos
Similar Questions
Explore conceptually related problems
RESONANCE ENGLISH-GRAVITATION-EXERCISE-2 PART-1
- Figure shows a spherical cavity inside a lead sphere. The surface of t...
Text Solution
|
- A straight of length L extends from x=a to x=L+a. the gravitational fo...
Text Solution
|
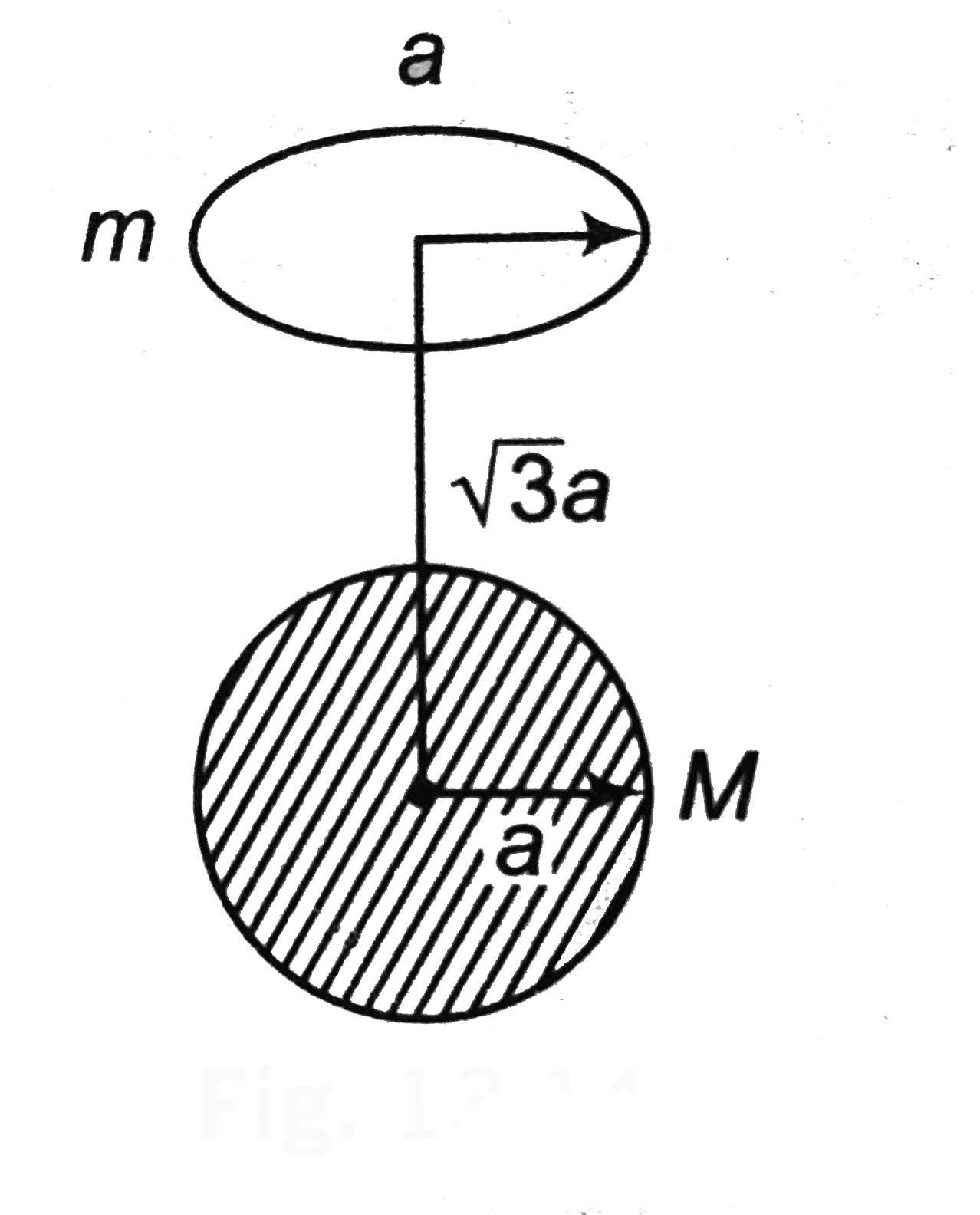
- A uniform ring of mass m is lying at a distance sqrt(3) a from the cen...
Text Solution
|
- The gravitational potential of two homogeneous spherical shells A and ...
Text Solution
|
- A projectile is fired vertically upwards from the surface of earth wit...
Text Solution
|
- Two small balls of mass m each are suspended side by side by two equal...
Text Solution
|
- A block of mass m is lying at a distance r from a spherical shell of m...
Text Solution
|
- In a spherical region the densiy varies inversely with the distance fr...
Text Solution
|
- The gravitational potential at a point outside the solid sphere of rad...
Text Solution
|
- A body of mass m is lifted up from the surface of earth to a height th...
Text Solution
|
- Assuming that the moon is a sphere of the same mean density as that of...
Text Solution
|
- A satellite can be in a geostationary orbit around earth in an orbit o...
Text Solution
|
- A geo-stationary satellite orbits around the earth in a circular orbit...
Text Solution
|
- A satellite of mass m revolves around the earth of radius R at a heigh...
Text Solution
|
- In Newton's inverse square law of gravitation had some dependence of r...
Text Solution
|