Topper's Solved these Questions
P-BLOCK ELEMENTS (HALOGEN & NOBLE GASES)
RESONANCE ENGLISH|Exercise EXERCISE-2 PART-3|15 VideosP-BLOCK ELEMENTS (HALOGEN & NOBLE GASES)
RESONANCE ENGLISH|Exercise EXERCISE-2 PART-4|16 VideosP-BLOCK ELEMENTS (HALOGEN & NOBLE GASES)
RESONANCE ENGLISH|Exercise EXERCISE-2 PART-1|16 VideosP-BLOCK ELEMENT (BORON AND CARBON FAMILY)
RESONANCE ENGLISH|Exercise PART - III : OLYMPIAD PROBLEMS (PREVIOUS YEARS) STAGE - V (INTERNATIONAL CHEMISTRY OLYMPIAD (IChO)) Problem 3|8 VideosPERIODIC TABLE & PERIODICITY
RESONANCE ENGLISH|Exercise Advanced Level Problems|105 Videos
Similar Questions
Explore conceptually related problems
RESONANCE ENGLISH-P-BLOCK ELEMENTS (HALOGEN & NOBLE GASES)-EXERCISE-2 PART-2
- The total number of electrons present in 4^"th" shell of Astatatine (....
Text Solution
|
- Predict the products when the following reactions are carried out (...
Text Solution
|
- A ball A of mass m falls on the surface of the earth from infinity. An...
Text Solution
|
- Predict the products when the following reactions are carried out (...
Text Solution
|
- Complete the reaction: underset"Conc."(HCl) + underset"Conc."(HNO3)to
Text Solution
|
- How many of the following reactions would have HCl as one of the prod...
Text Solution
|
- The number of mixed anhydride among the following are N2O3 , NO , N2O...
Text Solution
|
- A ball A of mass m falls on the surface of the earth from infinity. An...
Text Solution
|
- The number of lone pairs of electrons present in central atom of ClF3 ...
Text Solution
|
- Which selection is the correct formula for the chlorate ion?
Text Solution
|
- Chlorine water oxidises thiosulphates to:
Text Solution
|
- XeF2 + HCl rarr A+B+C
Text Solution
|
- The oxidation state of xenon in perxenate ion is +n. Give the value of...
Text Solution
|
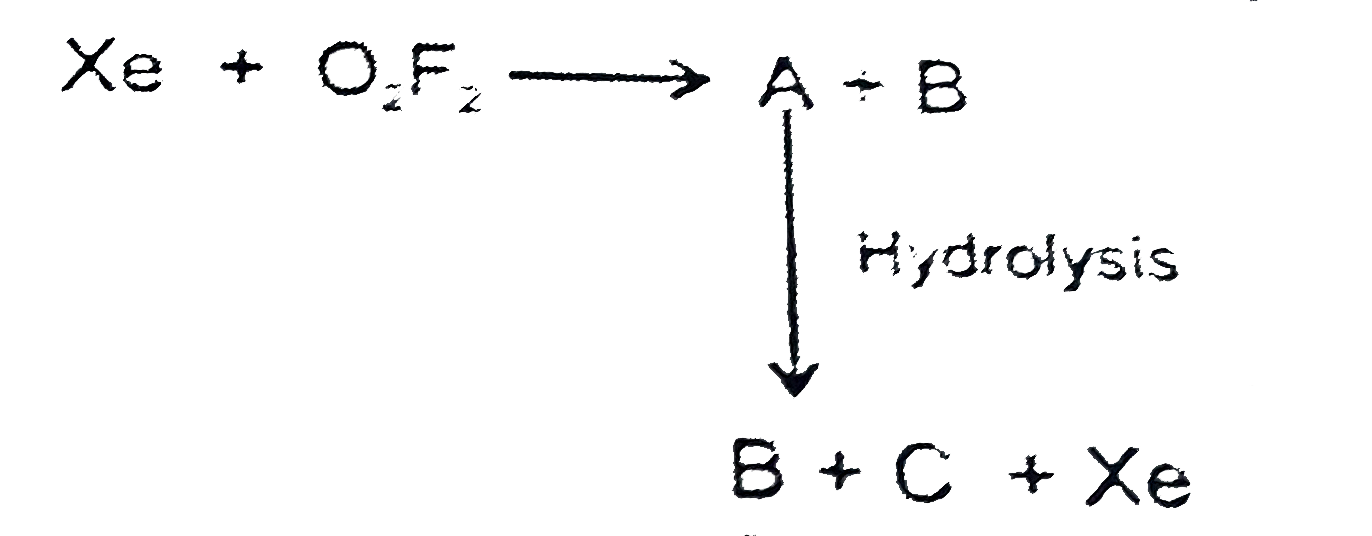
- A,B and C are:
Text Solution
|
- How many of the given compounds can produce XeO3. XeF6,XeF4, XeO2F...
Text Solution
|