Home
Class 12
MATHS
Let P(4, -4) and Q(9, 6) be two points o...

Let P(4, -4) and Q(9, 6) be two points on the parabola, `y^(2)=4x` and let X be any point on the are POQ of this parabola, where O is the vertex of this parabola, such that the area of `DeltaPXQ` is maximum. Then this maximum area (in sq. units) is

A

`31 3/4`

B

`30 1/2`

C

`32`

D

`31 1/4`

Text Solution

Verified by Experts

The correct Answer is:
D

`"The line AB is The distance of C from AB is :"`
`y+4=(10)/(5)(x-4)" "f(t)=(|2t^(2)-2t-12|)/(sqrt5)`
`y+4=2x-8" "=2(|(t-1//2)^(2)-(25)/(4)|)/(sqrt5)`
`" and "0let^(2)le 9 and -4 le 2t le 6`
`f(t)_("max")=t in [-2, 3] =2(25)/(4sqrt5)," Max area "rArr 2(25)/(4sqrt5)=(125)/(4)" sq. units."`
Promotional Banner

Topper's Solved these Questions

  • JEE MAIN REVISION TEST - 1 (2020)

    VMC MODULES ENGLISH|Exercise MATHEMATICS - SECTION 2|5 Videos

  • JEE MAIN REVISION TEST - 30 | JEE -2020

    VMC MODULES ENGLISH|Exercise MATHEMATICS|25 Videos

  • JEE MAIN REVISION TEST - 1 | JEE - 2020

    VMC MODULES ENGLISH|Exercise MATHEMATICS ( SECTION 2)|5 Videos

Similar Questions

Explore conceptually related problems

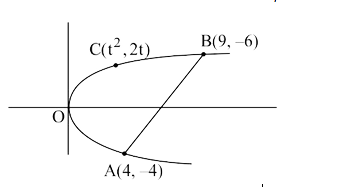
Let P(4,-4) and Q(9,6) be two points on the parabola, y^2=4x and let X be any point on the are POQ of this parabola, where O is the vertex of this parabola, such that the area of Delta PXQ is maximum. Then this maximum area (in square units) is (25k)/(4) . The value of k is

Let A(4,-4) and B(9,6) be points on the parabola y^(2)=4x. Let C be chosen on the on the arc AOB of the parabola where O is the origin such that the area of DeltaACB is maximum. Then the area (in sq. units) of DeltaACB is :

If the parabola y^(2) = 4ax passes through the point (4, 1), then the distance of its focus the vertex of the parabola is

P is parabola y^2=4ax and locus of mid points of all chords of this parabola passing through the vertex of P is a parabola P'. Axis of parabola P' will be

P is parabola y^2=4ax and locus of mid points of all chords of this parabola passing through the vertex of P is a parabola P'. Axis of parabola P' will be

Let (a,b) be a point on the parabola y=4x-x^(2) and is the point nearest to the point A(-1,4) Find (a+b).

Consider the parabola y^2=4xdot Let A-=(4,-4) and B-=(9,6) be two fixed points on the parabola. Let C be a moving point on the parabola between Aa n dB such that the area of the triangle A B C is maximum. Then the coordinates of C are (a) (1/4,1) (b) (4,4) (c) (3,2/(sqrt(3))) (d) (3,-2sqrt(3))

The line 4x+6y+9 =0 touches the parabola y^(2)=4ax at the point

Show that the locus of a point that divides a chord of slope 2 of the parabola y^2=4x internally in the ratio 1:2 is parabola. Find the vertex of this parabola.

Let P , Q and R are three co-normal points on the parabola y^2=4ax . Then the correct statement(s) is /at