Home
Class 12
MATHS
The length of the chord of the parabola ...

The length of the chord of the parabola `x^(2) = 4y` having equations `x - sqrt(2) y + 4 sqrt(2) = 0` is

A

`8sqrt(2)`

B

`2sqrt(11)`

C

`6sqrt(3)`

D

`3sqrt(2)`

Text Solution

Verified by Experts

The correct Answer is:
C

`x^(2)=4y .....(i)`
`x-sqrt(2)y+4sqrt(2)=0`
`x=sqrt(2)y-4sqrt(2).......(ii)`
For Point of intersection we will solve both the equation
`(sqrt(2)y-4sqrt(2))^(2)=4y`
`2y^(2)+32-16y=4y`
`y^(2)-10y+16=0`
`y^(2)-2y-8y+16=0`
`(y-2)(y-8)=0`
`y=2, y=8`
`x^(2)=8`
`x=pm 2sqrt(2)`
`A=-2sqrt(2),2)`
`x^(2)=32`
`x=pm 4sqrt(2)`
`B(4 sqrt(2),8)`
`"(dist)"_(AB)=sqrt((4sqrt(2)-(-2sqrt(2)))^(2)+(8-2)^(2))`
`=sqrt(36xx2+36)`
dist `=6sqrt(3)`
Promotional Banner

Topper's Solved these Questions

  • JEE MAIN REVISION TEST-3 (2020)

    VMC MODULES ENGLISH|Exercise MATHEMATICS (SECTION 2)|5 Videos

  • JEE Main Revision Test-20 | JEE-2020

    VMC MODULES ENGLISH|Exercise MATHEMATICS|25 Videos

  • JEE Main Revision Test-6 | JEE-2020

    VMC MODULES ENGLISH|Exercise MATHEMATICS|25 Videos

Similar Questions

Explore conceptually related problems

The mid-point of the chord 2x+y-4=0 of the parabola y^(2)=4x is

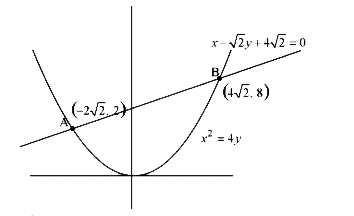
The length of the chord of the parabola y^2=x which is bisected at the point (2, 1) is (a) 2sqrt(3) (b) 4sqrt(3) (c) 3sqrt(2) (d) 2sqrt(5)

Show that the equation of the chord of the parabola y^2 = 4ax through the points (x_1, y_1) and (x_2, y_2) on it is : (y-y_1) (y-y_2) = y^2 - 4ax

STATEMENT-1 : The length of latus rectum of the parabola (x - y + 2)^(2) = 8sqrt(2){x + y - 6} is 8sqrt(2) . and STATEMENT-2 : The length of latus rectum of parabola (y-a)^(2) = 8sqrt(2)(x-b) is 8sqrt(2) .

The length of the latus - rectum of the parabola 4y^(2) + 2x - 20 y + 17 = 0 is

Find the length of the common chord of the parabola y^2=4(x+3) and the circle x^2+y^2+4x=0 .

Find the length of the common chord of the parabola y^2=4(x+3) and the circle x^2+y^2+4x=0 .

Find the equation of the chord of the parabola y^(2)=8x having slope 2 if midpoint of the chord lies on the line x=4.

The length of latus-rectum of the hyperbola x^(2) - 2y ^(2) - 2x + 8y - 1 = 0 is (i) sqrt(6) (ii) 4 sqrt(3) (iii) 4 (iv) 3

The equation of the chord of the ellipse x^(2) + 4y^(2) = 4 having the middle point at (-2, (1)/(2)) is