Home
Class 12
MATHS
A circle cuts a chord of length 4a on th...

A circle cuts a chord of length 4a on the x-axis and passes through a point on the y-axis, distant 2b from the origin. Then the locus of the centre of this circle is

A

A parabola

B

A hyperbola

C

A straight line

D

An elipse

Text Solution

Verified by Experts

The correct Answer is:
A
In `Delta ACM:`
`K ^(2) + 4a ^(2) =r ^(2) " "…(i)`
`h ^(2) + (K-2b)^(2) =r ^(2) " "…(ii)`
`K ^(2) + 4a ^(2) = h^(2) + (K -2b )^(2) `
`K ^(2) + 4a ^(2) =h^(2)+ K^(2) + 4b ^(2) -4Kb`
`therefore h ^(2) =4Kb + 4a ^(2) -4b ^(2)`
`x ^(2)=4by+ 4a ^(2) -4b ^(2)`
`therefore ` Parabola.
Promotional Banner

Topper's Solved these Questions

  • JEE MAIN REVISION TEST 5 (2020)

    VMC MODULES ENGLISH|Exercise MATHEMATICS (SECTION 2)|5 Videos

  • JEE MAIN REVISION TEST 11 (2020)

    VMC MODULES ENGLISH|Exercise MATHEMATICS (SECTION - 2)|4 Videos

  • JEE MAIN REVISION TEST 8 (2020)

    VMC MODULES ENGLISH|Exercise MATHEMATICS ( SECTION 2 )|5 Videos

Similar Questions

Explore conceptually related problems

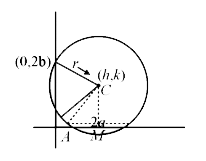
Prove that the locus of the center of a circle, which intercepts a chord of given length 2a on the axis of x and passes through a given point on the axis of y distant b from the origin, is a parabola.

Find the equations of the circles passing through two points on y-axis at distance 3 from the origin and having radius 5.

The equation of the circle whose radius is 5 and which passes through the points on x-axis at a distance 3 from the origin is

A circle cuts the chord on x-axis of length 4a . If this circle cuts the y-axis at a point whose distance from origin is 2b . Locus of its centre is (A) Ellipse (B) Parabola (C) Hyperbola (D) Straight line

Find the equation of the circle which passes through two points on the x-axis which are at distances 4 from the origin and whose radius is 5.

A variable circle passes through the fixed point (2, 0) and touches y-axis Then, the locus of its centre, is

A variable circle passes through the fixed point (2, 0) and touches y-axis Then, the locus of its centre, is

A line is at a distance c from origin and meets axes in A and B. The locus of the centre of the circle passing through O,A,B is

The smallest circle with centre on y-axis and passing through the point (7,3) has radius

If a circle passes through the point (a,b) and cuts the circle x^2+y^2=k^2 orthogonally then the locus of its centre is