Home
Class 12
PHYSICS
Two particles A,B are moving on two conc...

Two particles A,B are moving on two concentric circles of radii `R_1` and `R_2` with equal angular speed `omega`. At`t=0`,their positions and direction of motion are shown in the figure. The relative velocity `vecV_a-vecV_b` at `t=pi//2omega` is given by :

A

`omega (R_(1) - R_(2)) hat(i)`

B

`omega(R_(1) + R_(2)) hat(i)`

C

`-omega(R_(1) + R_(2))hat(i)`

D

`omega(R_(2) - R_(1))hat(i)`

Text Solution

Verified by Experts

The correct Answer is:
D
At `t = (pi)/(2 omega), theta = omega t = (pi)/(2)`. Hence the position of A and B would be
`vec(V)_(A) = R_(1) omega(-hat(i))`
`vec(V)_(B) = R_(2)omega(-hat(i))`
`vec(V)_(A) - vec(V)_(B) = (R_(1)omega - R_(2) omega)(-hat(i))`
Or `vec(V)_(A) - vec(V)_(B) = (R_(2) - R_(1)) omega (hat(i))`
Promotional Banner

Topper's Solved these Questions

  • JEE MAIN REVISION TEST - 7|JEE - 2020

    VMC MODULES ENGLISH|Exercise Physics (Section -2) (Numerical Value Type)|5 Videos

  • JEE MAIN REVISION TEST - 4 JEE - 2020

    VMC MODULES ENGLISH|Exercise PHYSICS|25 Videos

  • JEE MAIN REVISION TEST -14

    VMC MODULES ENGLISH|Exercise PHYSICS (SECTON 2)|5 Videos

Similar Questions

Explore conceptually related problems

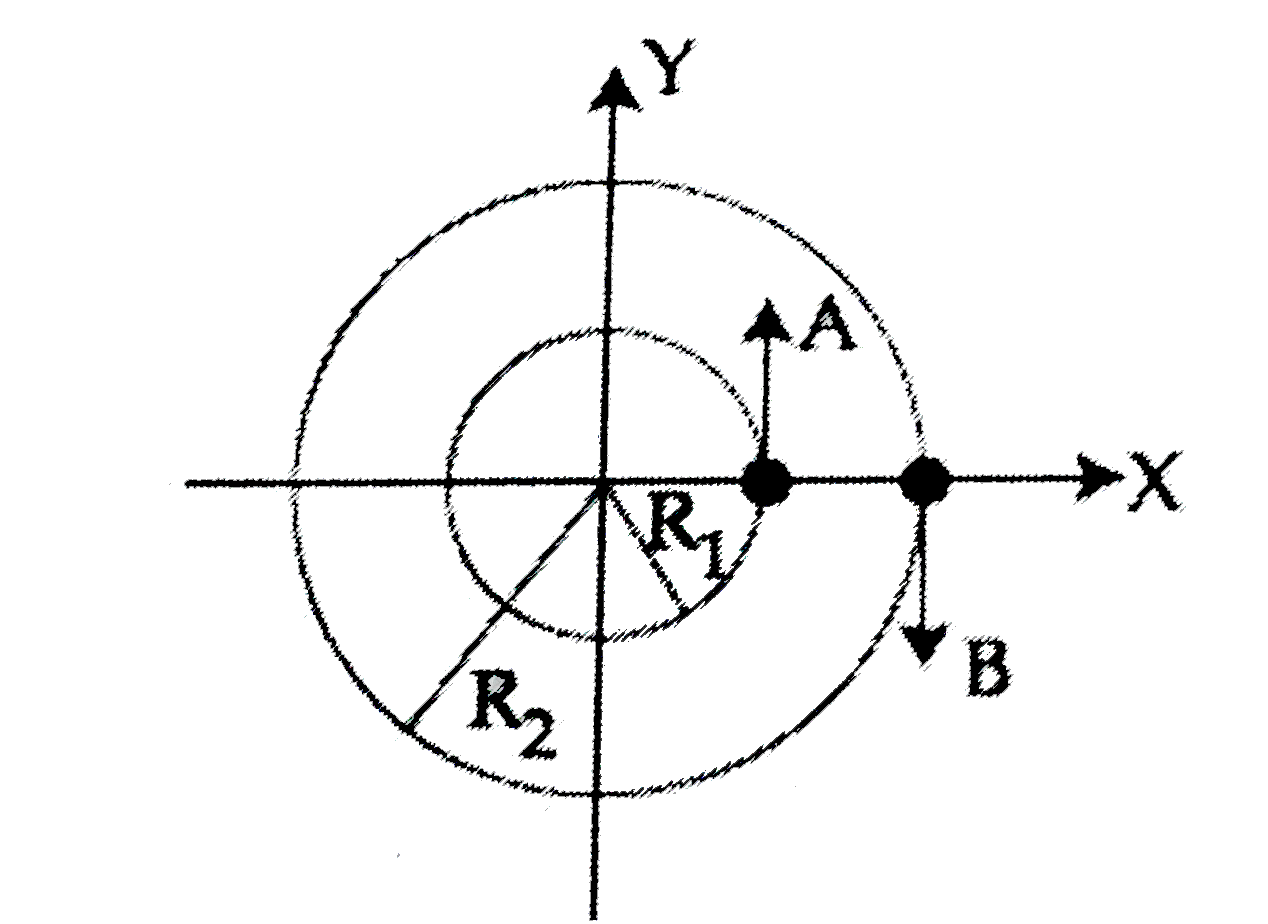
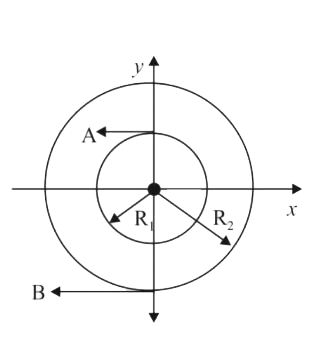
Two particles A and B are moving in uniform circular motion in concentric circles of radii r_(A) and r_(B) with speed u_(A) and u_(B) respectively. Their time period of rotation is the same. The ratio of angular speed of a to that of B will be:

Two particles A and B are revolving with constant angular velocity on two concentric circles of radius 1m and 2m respectively as shown in figure. The positions of the particles at t = 0 are shown in figure. The positions of the particles at t=0 are shown in figure. if m_(A)=2kg, m_(B)= 1kg and vec(P)_(A) and vec(P)_(B) are linear momentum of the particle then what is the maximum value of |vec(P)_(A)+vec(P)_(B)| in kg-m/sec in subsequent motion of two particles.

Two particle move in concentric circles of radii r_(1) and r_(2) such that they maintain a straight line through the center. The ratio of their angular velocities is:

Two particles P and Q are moving as shown in the figure. At this moment of time the angular speed of P w.r.t. Q is

The magnitude of displacement of a particle moving in a circle of radius a with constant angular speed omega varries with time t is

Two particles A and B are moving as shown in figure. At this moment of time, the angular speed of A with respect to B is?

A particle moves along a circle of radius R with a constant angular speed omega . Its displacement (only magnitude) in time t will be

Two particles A and B are moving in a horizontal plane anitclockwise on two different concentric circles with different constant angular velocities 2omega and omega respectively. Find the relative velocity (in m/s) of B w.r.t. A after tome t=pi//omega . They both start at the position as shown in figure ("Take" omega=3rad//sec, r=2m)

Two particles are moving in different circles in same plane with different angular velocities as shown in figure. At t = 0, initial positions of particles A and B are shown by dots on the respective circles. Initial distance between particles is 1m. Particle A move anticlockwise in the first circle whereas B moves clockwise in the second circle. Angle described (rotated) by A and B in time 't' are theta_(A)=((pi)/2t) and theta_(B)=(pit) respectively. here theta is in radian and t is in second. Radius of each circle is shown in diagram. At time t=2 second, the angular velocity of the particle A with respect to the particle B is

A and B are moving in two circular orbits with angular velocity 2 omega and omega respectively. Their position are shown at t = 0. Find the time at which they will meet for 1st time