A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
VMC MODULES ENGLISH-JEE MAIN REVISION TEST 8 (2020)-MATHEMATICS ( SECTION 2 )
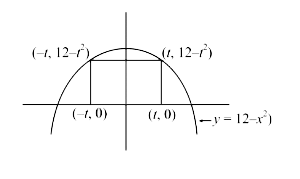
- Find the are of the largest rectangle with lower base on the x-axis ...
Text Solution
|
- If the straight line 2x-3y+17=0 is perpendicular to the line passing t...
Text Solution
|
- Ratio of the 5^(th) term from the beginning to the 5^(th) term from th...
Text Solution
|
- Let P(4,-4) and Q(9,6) be two points on the parabola, y^2=4x and let X...
Text Solution
|
- Let C(1) " and" C(2) be the centres of the circles x^(2)+y^(2)-2x-2y-2...
Text Solution
|
- If lambda be the ratio of the roots of the quadratic equation in x, 3m...
Text Solution
|
 .
.