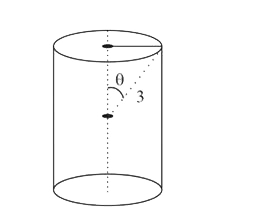
A
B
C
D
Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
VMC MODULES ENGLISH-JEE Main Revision Test-9 | JEE-2020 -SECTION 2
- The height of a right circular cylinder of maxium volume inscribed in ...
Text Solution
|
- The sum sum ( k = 1 ) ^ ( 20 ) k ( 1 ) / ( 2 ^ k ) is equa...
Text Solution
|
- The tangent and the normal lines at the point (sqrt3, 1) to the circle...
Text Solution
|
- The number of four-digit numbers strictly greater than 4321 that can b...
Text Solution
|
- Let f : R to R be a differentiable function satisfying f'(3) + f'(2) ...
Text Solution
|
- Suppose that the points (h,k), (1,2) and (-3,4) lie on the line L(1). ...
Text Solution
|