Home
Class 12
MATHS
ABC is a triangular park with AB=AC=100 ...

ABC is a triangular park with AB=AC=100 m .A clock tower is situated at the midpoint of BC. The angle of elevation `alpha " and " beta ` of the top of the tower at A and B, respectively ,are such that cot `alpha` =3.2 cosec `beta` = 2.6 Find the height of the tower .

A

`100/(3sqrt(3))`

B

25

C

20

D

`10sqrt(5)`

Text Solution

Verified by Experts

The correct Answer is:
C
Let h(m) be the height of the tower
Say BM=d

`theta = "cosec"^(-1)2sqrt(2)`
`2sqrt(2) =(sqrt(d)^(2)-d^(2))/h`
`cot phi =sqrt((100)^(2)-d^(2))/h`
`3sqrt(2)=sqrt((100)^(2)-d^(2))/h`
`18h^(2) = 100^(2)-d^(2)`...........(2)

Put the values of `d^(2)` from (1) and (2)
`18h^(2) = 100^(2) -7h^(2) rArr 25h^(2) = 100 xx 100`
h=20 m
Promotional Banner

Topper's Solved these Questions

  • JEE MAIN REVISION TEST -14

    VMC MODULES ENGLISH|Exercise MATHEMATICS (SECTION 2)|5 Videos

  • JEE MAIN REVISION TEST - 7|JEE - 2020

    VMC MODULES ENGLISH|Exercise Mathematics (Section - 2) Numercial type questions|5 Videos

  • JEE MAIN REVISION TEST -17 (2020)

    VMC MODULES ENGLISH|Exercise MATHEMATICS|25 Videos

Similar Questions

Explore conceptually related problems

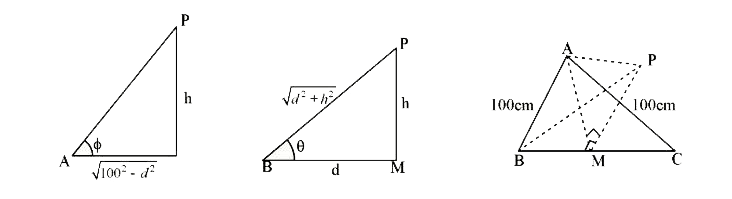
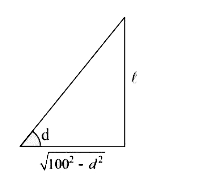
ABC is a triangular park with AB = AC = 100 m. A block tower is situated at the midpoint of BC.The angles of elevation of the top of the tower at A and B are cot^-1(3.2) and cosec^-1(2.6) respectively.The height of the tower is:

PQR is a triangular park with PQ=PR=200m . A T.V tower stands at the mid-point of QR. If the angles of elevation of the top of the tower at P , Q and R respectively 45^@ , 30^@ and 30^@ then the height of the tower in m is

PQR is a triangular park with PQ=PR=200m . A T.V tower stands at the mid-point of QR. If the angles of elevation of the top of the tower at P , Q and R respectively 45^@ , 30^@ and 30^@ then the height of the tower in m is

PQR is a triangular park with PQ=PR=200m . A.T.V. tower stands at the mid-point of QR . If the angles of elevation of the top of the tower at P , Q and R are respectively 45^(ulo) , 30^(ulo) and 30^(ulo) then the height of the tower (in m ) is

The persons are standing on the opposite sides of a tower. They observe the angles of elevation of the top of the tower to be 30^(@) and 38^(@) respectively. Find the distance between them, if the height of the tower is 50 m

The angles of the depression of the top and bottom of the tower is seen from the top of a 60sqrt(3) cliff are 45^alpha and 60^alpha respectively. Find the height of the tower.

The angles of the depression of the top and bottom of the tower is seen from the top of a 60sqrt(3) cliff are 45^alpha and 60^alpha respectively. Find the height of the tower.

The angles of the depression of the top and bottom of the tower is seen from the top of a 60sqrt(3) cliff are 45^alpha and 60^alpha respectively. Find the height of the tower.

The angle of elevation of the top of a tower. from a point on the ground and at a distance of 160 m from its foot, is fond to be 60^(@) . Find the height of the tower .

If figure, the angle of elevation of the top of a tower from a point C on the ground which is 30 m away from the foot of the tower, is 30^(@) . Find th height of the tower.