Home
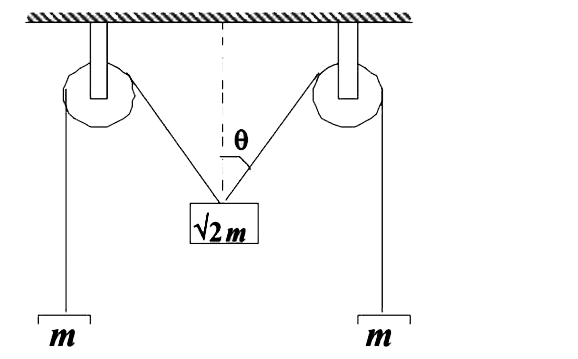
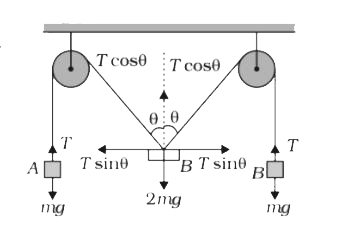
Class 12
PHYSICS
The pulleys and strings shown in the fig...

The pulleys and strings shown in the figure are smooth and of negligible mass. For the system to remain in equilibrium, the angle `theta` should be

A

(a)`0^(@)`

B

(b)`30^(@)`

C

(c)`45^(@)`

D

(d)`60^(@)`

Text Solution

Verified by Experts

The correct Answer is:
c
For vertical equilibrium of the block `f= mg =0.98 N lt (f)_(max) sqrt(2)mg =2T cos theta =2 (mg) cos theta `
`because` T=m g at equilibrium )
`because T=mg therefore cos theta =(1)/sqrt(2) rar theta =45^(@)`
Promotional Banner

Topper's Solved these Questions

  • INTRODUCTION TO VECTORS & FORCES

    VMC MODULES ENGLISH|Exercise JEE Main ( ARCHIVE ) ( LEVEL-1)|12 Videos

  • GRAVITATION

    VMC MODULES ENGLISH|Exercise JEE Advance (Archive) TRUE/FALSE|1 Videos

  • JEE MAIN - 5

    VMC MODULES ENGLISH|Exercise PART I : PHYSICS (SECTION - 2)|5 Videos

Similar Questions

Explore conceptually related problems

The pulleys and strings shown in fig are smooth and of negligible mass. For the system to remain in equilibrium the angle theta should be:

The pulley and strings shown in fig 15.3.16 are smooth and of negligible mass. For the system to remiain in equilibrium the angle theta should be

The system is in equilibrium. Find the angle theta

In the given arrangement, for the system to remain under equilibrium, the ' theta ' should be:

A smooth rod length l is kept inside a trolley at an angle theta as shown in the figure. What should be the acceleration a of the trolley so that the rod remain in equilibrium with respect to it?

For the system shown in figure , to be in equilibrium , determine mass m .

For the system shown in figure, the tensions in the string

Two masses m and M are attached to the strings as shown in the figure. If the system is in equilibrium, then

For the equilibrium of the system shown, the value of mass m should be

Three masses m_1 = m ,m_2 = 2m and m_3 = 3m are hund on a string passing over a frictionless pulley as shown in Figure . The mass of the string in negligible . The system is released from rest. The tension in the string between masses m_2 and m_3 is