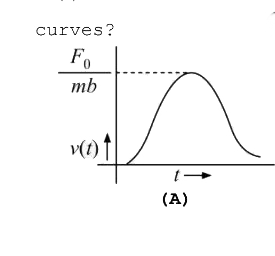
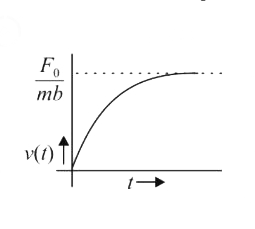
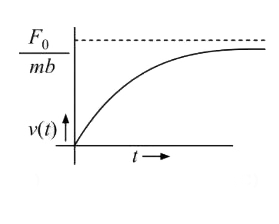
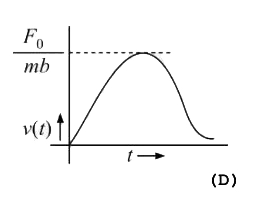
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
DYNAMICS OF A PARTICLE
VMC MODULES ENGLISH|Exercise JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )|31 VideosDYNAMICS OF A PARTICLE
VMC MODULES ENGLISH|Exercise LEVEL 2 ( NUMERICAL TYPE FOR JEE MAIN )|16 VideosDC CIRCUIT
VMC MODULES ENGLISH|Exercise JEE ADVANCED ARCHIVE|68 VideosELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
VMC MODULES ENGLISH|Exercise IN-CHAPTER EXERCISE-G|10 Videos
Similar Questions
Explore conceptually related problems
VMC MODULES ENGLISH-DYNAMICS OF A PARTICLE-JEE Main (Archive) Level - I
- A machine gun fires a bullet of mass 40 g with a velocity 1200 ms^(-1)...
Text Solution
|
- Two masses m1=5kg and m2=4.8kg tied to a string are hanging over a lig...
Text Solution
|
- A particle is acted upon by a force of constant magnitude which is alw...
Text Solution
|
- A block is kept on a frictionless inclined surface with angle of incli...
Text Solution
|
- A particle of mass 0.3 kg subject to a force F=-kx with k=15N//m. What...
Text Solution
|
- A smooth block is released at rest on a 45^@ incline and then slides a...
Text Solution
|
- Consider a car moving on a straight road with a speed of 100m//s. The ...
Text Solution
|
- The upper half of an inclined plane of inclination theta is perfectly ...
Text Solution
|
- A player caught a cricket ball of mass 150g moving at a rate of 20m//s...
Text Solution
|
- A ball of mass 0.2 kg is thrown vertically upwards by applying a force...
Text Solution
|
- A block of mass 'm' is connected to another block of mass 'M' by a spr...
Text Solution
|
- A body of mass m = 3.513 kg is moving along the x-axis with a speed of...
Text Solution
|
- Two fixed frictionless inclined plane making an angle 30^(@) and 60^(@...
Text Solution
|
- A particle of mass m is at rest the origin at time t= 0 . It is subj...
Text Solution
|
- A body starts from rest on a long inclined plane of slope 45^(@) . The...
Text Solution
|
- Two blocks of mass M(1) = 20 kg and M(2) = 12 kg are connected by a ...
Text Solution
|
- A block is placed on a rough horizontal plane. A time dependent horizo...
Text Solution
|
- A block of mass is placed on a surface with a vertical cross section g...
Text Solution
|
- A body with mass 5 kg is acted upon by a force F=(-3 hati+4 hatj)N. If...
Text Solution
|
- A block A of mass 4 kg is placed on another block B of mass 5 kg , and...
Text Solution
|