Home
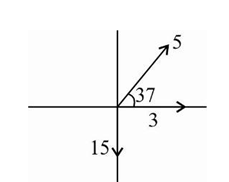
Class 12
PHYSICS
The resultant amplitude due to superposi...

The resultant amplitude due to superposition of three simple harmonic motions `x_(1) = 3sin omega t`,
`x_(2) = 5sin (omega t + 37^(@))` and `x_(3) = - 15cos omega t` is

A

18

B

10

C

12

D

none of

Text Solution

Verified by Experts

The correct Answer is:
D
`x_(1)=3sinomegat`
`x_(2)=5sin(omegat+37^(@))`
`x_(3)=15sin(omegat+pi+(pi)/(2))`
`A_(R)=sqrt(A_(x)^(2)+A_(y)^(2))=sqrt((7)^(2)+(12)^(2))=sqrt(49+144)=sqrt(193)`
Promotional Banner

Topper's Solved these Questions

  • SIMPLE HARMONIC MOTION

    VMC MODULES ENGLISH|Exercise 6-previous year question|56 Videos

  • SIMPLE HARMONIC MOTION

    VMC MODULES ENGLISH|Exercise 7-previous year question|46 Videos

  • SIMPLE HARMONIC MOTION

    VMC MODULES ENGLISH|Exercise LEVEL (1)|75 Videos

  • ROTATIONAL MOTION

    VMC MODULES ENGLISH|Exercise JEE Advanced (Archive) (True/False Type)|3 Videos

  • SYSTEM OF A PARTICLES & ROTATIONAL MOTION

    VMC MODULES ENGLISH|Exercise IN-CHAPTER EXERCISE F|10 Videos

Similar Questions

Explore conceptually related problems

x_(1) = 5 sin omega t x_(2) = 5 sin (omega t + 53^(@)) x_(3) = - 10 cos omega t Find amplitude of resultant SHM.

x_(1) = 5 sin omega t x_(2) = 5 sin (omega t + 53^(@)) x_(3) = - 10 cos omega t Find amplitude of resultant SHM.

Find the displacement equation of the simple harmonic motion obtained by combining the motion. x_(1) = 2sin omega t , x_(2) = 4sin (omega t + (pi)/(6)) and x_(3) = 6sin (omega t + (pi)/(3))

If i_(1)=3 sin omega t and (i_2) = 4 cos omega t, then (i_3) is

Determine resultant amplitude after super position of given four waves with help of phasor diagram. y_(1) = 15 sin omega t mm,y_(2) = 9 sin (omega t -pi//2) mm,y_(3)=7 sin (omega t +pi//2)mm & y_(4) = 13 sin omega t mm .

A partical is subjucted to two simple harmonic motions x_(1) = A_(1) sin omega t and x_(2) = A_(2) sin (omega t + pi//3) Find(a) the displacement at t = 0 , (b) the maximum speed of the partical and ( c) the maximum acceleration of the partical.

Two simple harmonic motions given by, x = a sin (omega t+delta) and y = a sin (omega t + delta + (pi)/(2)) act on a particle will be

The equation of the resultant motion of the number of simple harmonic motions is E_(c)=(1+K sin omega_(2)t) sin omega_(1)t . The number of simple harmonic components is/are.

Two particle A and B execute simple harmonic motion according to the equation y_(1) = 3 sin omega t and y_(2) = 4 sin [omega t + (pi//2)] + 3 sin omega t . Find the phase difference between them.

Find the resultant amplitude and the phase difference between the resultant wave and the first wave , in the event the following waves interfere at a point , y_(1) = ( 3 cm) sin omega t , y_(2) = ( 4 cm) sin (omega t + (pi)/( 2)), y_(3) = ( 5 cm ) sin ( omega t + pi)

VMC MODULES ENGLISH-SIMPLE HARMONIC MOTION -LEVEL (2)
  1. A simple pendulum of length l is suspended in a car that is travelling...

    Text Solution

    |

  2. If the length of a simple pendulum is equal to the radius of the earth...

    Text Solution

    |

  3. A uniform dics of mass m and radius R=(80)/(23pi^2)m is pivoted smooth...

    Text Solution

    |

  4. What is the period of oscillation of a liquid contained in a U - tube ...

    Text Solution

    |

  5. A disc of mass M = 4 kg, radius R = 1 m is attached with two blocks A ...

    Text Solution

    |

  6. Consider the situation in which one end of a massless spring of spring...

    Text Solution

    |

  7. A solid cylinder of mass m is attached to a horizontal spring with for...

    Text Solution

    |

  8. Consider the situation in which one end of a massless spring of spring...

    Text Solution

    |

  9. In the Column I, a system is described in each option and correspondin...

    Text Solution

    |

  10. A uniform disc of mass m and radius R is pivoted smoothly at its centr...

    Text Solution

    |

  11. The angular frequency of a spring block system is omega(0). This syste...

    Text Solution

    |

  12. Vertical displacement of a plank with a body of mass m on it is varyin...

    Text Solution

    |

  13. The coefficient of friction between block of mass m and 2m is mu=2tant...

    Text Solution

    |

  14. A body of mass m is released from a height h to a scale pan hung from ...

    Text Solution

    |

  15. The resultant amplitude due to superposition of three simple harmonic ...

    Text Solution

    |

  16. A coin is placed on a horizontal platform, which undergoes horizontal ...

    Text Solution

    |

  17. Two identical blocks A and B, each of mass m=3kg, are connected with t...

    Text Solution

    |

  18. Two identical blocks A and B, each of mass m=3kg, are connected with t...

    Text Solution

    |

  19. Two identical blocks A and B, each of mass m=3kg, are connected with t...

    Text Solution

    |

  20. In the figure shown mass 2m is at rest and in equilibrium. A particle ...

    Text Solution

    |