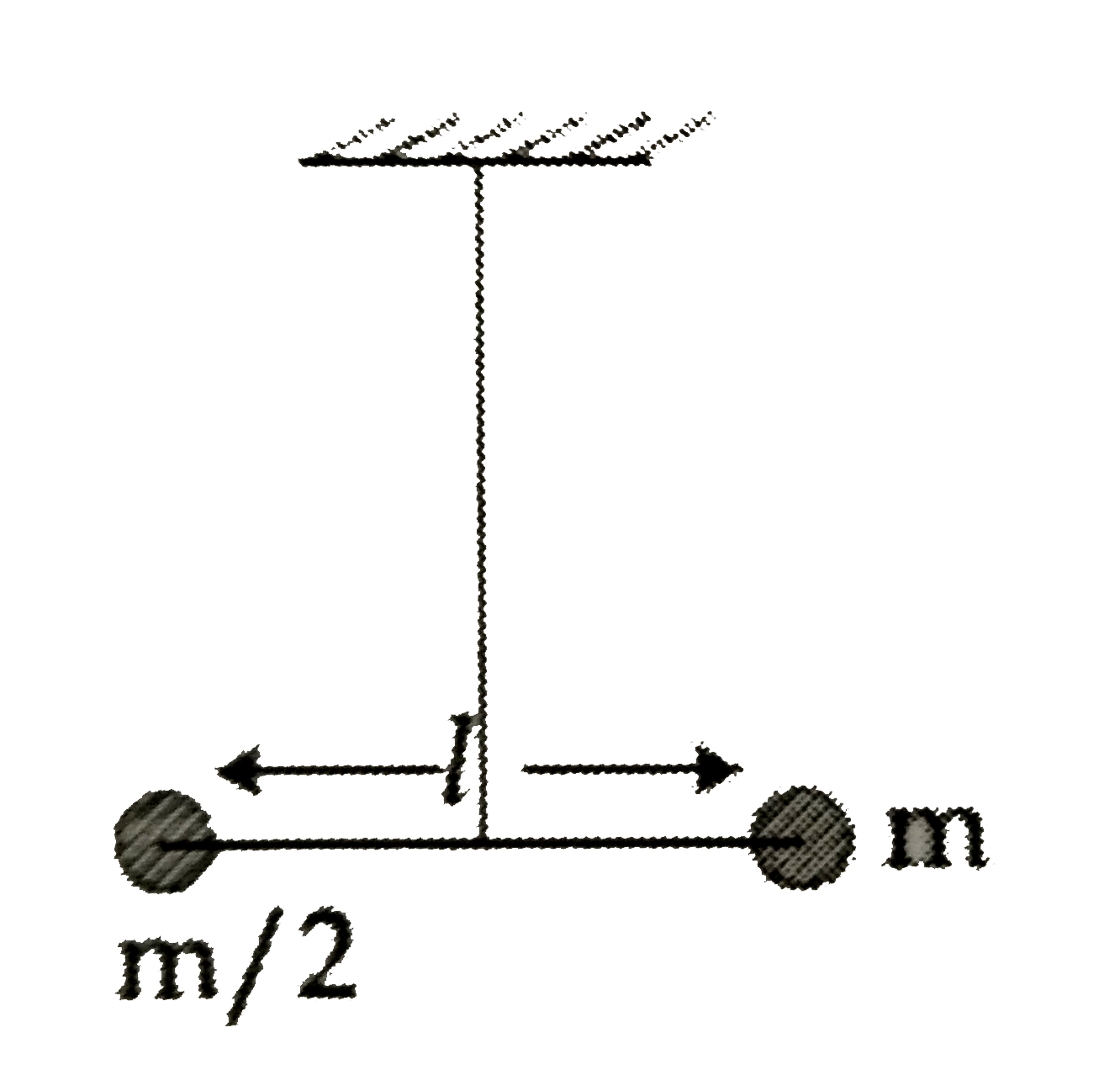
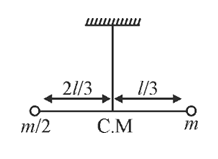
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
SIMPLE HARMONIC MOTION
VMC MODULES ENGLISH|Exercise 7-previous year question|46 VideosSIMPLE HARMONIC MOTION
VMC MODULES ENGLISH|Exercise LEVEL (2)|40 VideosROTATIONAL MOTION
VMC MODULES ENGLISH|Exercise JEE Advanced (Archive) (True/False Type)|3 VideosSYSTEM OF A PARTICLES & ROTATIONAL MOTION
VMC MODULES ENGLISH|Exercise IN-CHAPTER EXERCISE F|10 Videos
Similar Questions
Explore conceptually related problems
VMC MODULES ENGLISH-SIMPLE HARMONIC MOTION -6-previous year question
- A silver atom in a solid oscillates in simple harmonic motion in some ...
Text Solution
|
- The position co-ordinates of a particle moving in a 3-D coordinate sys...
Text Solution
|
- A particle is executing simple harmonic motion (SHM) of amplitude A, a...
Text Solution
|
- A rod of mass 'M' and length '2L' is suspended at its middle by a wire...
Text Solution
|
- A block of mass m, lying on a smooth horizontal surface, is attached t...
Text Solution
|
- A particle excutes simple harmonic motion with an amplitude of 5 cm. W...
Text Solution
|
- The mass and the diameter of a planet are three times the repective v...
Text Solution
|
- A pendulum is executing simple harmonic motion and its maximum kinet...
Text Solution
|
- A simple harmonic motion is represented by : y=5(sin3pit+sqrt(3)cos3...
Text Solution
|
- A simple pendulum , made of a string of length l and a bob of ma...
Text Solution
|
- two light identical springs of spring constant K are attached horizon...
Text Solution
|
- A damped harmonic oscillator has a frequency of 5 oscillations per se...
Text Solution
|
- A simple pendulum oscillating in air has period T. The bob of the pend...
Text Solution
|
- A massless spring (K=800 N/m), attached with a mass (500g) is complete...
Text Solution
|
- Equation of motion for a particle performing damped harmonic oscillati...
Text Solution
|
- A uniform spring whose unstretched length is l has a force constant k....
Text Solution
|
- A cylindrical plastic bottle of negligible mass is filled with 310 ml ...
Text Solution
|
- A body is of mass 1 kg falls freely from a height of 100 m. on a platf...
Text Solution
|
- A particle undergoing simle harmonic motion has time dependent displac...
Text Solution
|
- Two masses m and (m)/(2) are connected at the two ends of a massless r...
Text Solution
|