Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
VMC MODULES ENGLISH-SIMPLE HARMONIC MOTION -7-previous year question
- When a particle is mass m moves on the x- axis in a potential of the f...
Text Solution
|
- When a particle is mass m moves on the x- axis in a potential of the f...
Text Solution
|
- When a particle is mass m moves on the x- axis in a potential of the f...
Text Solution
|
- Phase space diagrams are useful tools in analysing all kond of dynamic...
Text Solution
|
- Phase space diagrams are useful tools in analyzing all kinds of dynami...
Text Solution
|
- Phase space diagrams are useful tools in analyzing all kinds of dynami...
Text Solution
|
- Column I gives some devices and Column II given some processes on whic...
Text Solution
|
- Column I gives a listof possible set of parameters measured in some ex...
Text Solution
|
- A mass (M) attached to a spring, oscillates with a period of (2 sec). ...
Text Solution
|
- A block is kept on a horizontal table. The table is undergoing simple ...
Text Solution
|
- A particle executes S.H.M. between x = -A and x = + A. The time taken ...
Text Solution
|
- A 0.1 kg mass is suspended from a wire of negligible mass. The length...
Text Solution
|
- A spring-block system is resting on a frictionless floor as shown in t...
Text Solution
|
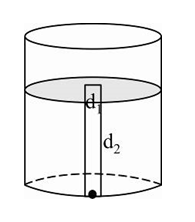
- An ideal gas enclosed in a vertical cylindrical container supports a f...
Text Solution
|
- Two masses m 1 and m 2 are suspended together by a massless spring of ...
Text Solution
|
- The equations of displacement of two waves are y(1)=10"sin"(3pit+pi...
Text Solution
|
- The velocity of the liquid coming out of a small hole of a vessel cont...
Text Solution
|
- An object of mass 0.2 kg executes simple harmonic oscillation along th...
Text Solution
|
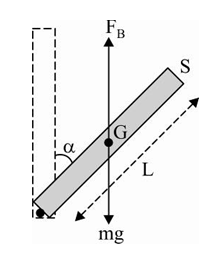
- A thin rod of length L and area of cross section S is pivoted at its l...
Text Solution
|
- A mass m is undergoing SHM in the verticl direction about the mean pos...
Text Solution
|