In figure (a) three capacitors of capacitances `C_(1),C_(2),C_(3)` are connected in series between point A and D.
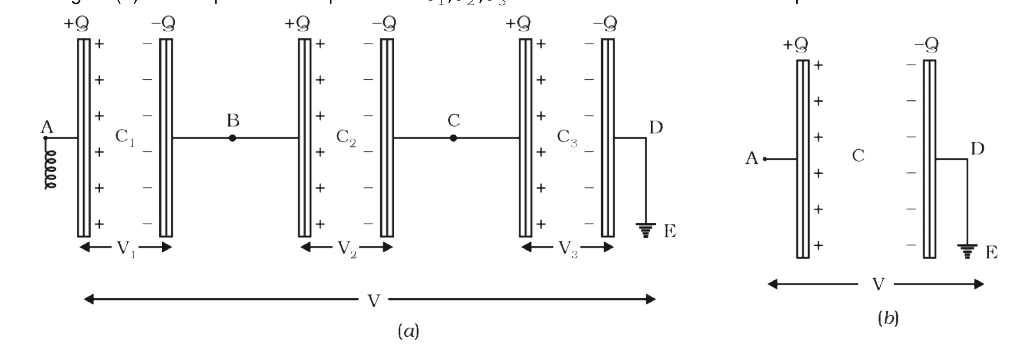
In series first plate of each capacitor has charge + Q and second plate of each capacitor has change –Q i.e,, charge on each capacitor is Q .
Let the potential differences across the capacitors `C_(1),C_(2),C_(3)` be `V_(1),V_(2),V_(3)` respectively. As the second plate of first capacitors `C_(1)` and first plate of second capacitor `C_(2)` are connected together, their potentials are equal. Let this common potential be `V_(B)`. Similarly the common potential of second plate of `C_(2)` and first plate of `C_(3)` is `V_(C)`. the second plate of capacitor `C_(3)` is connected to each , therefore its potential As charge flows from higher potential to lower potential, therefore, `V_(A) gt V_(B) gt C_(V) gt V_(D)`.
For first capacitor, `V_(1)=V_(A)-V_(B)=(Q)/(C_(1))` . .. (i)
For second capacitor, `V_(2)=V_(B)-V_(C)=(Q)/(C_(2))0` . . (ii)
For this capacitor, `V_(3)=V_(C)-V_(D)=(Q)/(C_(3))` . . (iii)
Addition equations (i), (ii), (iii) we get `V_(1)+V_(2)+V_(3)=V_(A)-V_(D)=[(1)/(C_(1))+(1)/(C_(2))+(1)/(C_(3))]Q` . . (iv)
If V be the potential difference betweenn A and D, then `V_(A)-V_(D)=V`
`therefore`From (iv), we get `V=(V_(1)+V_(2)+V_(3))=Q[(1)/(C_(1))+(1)/(C_(2))+(1)/(C_(3))]` . . (v)
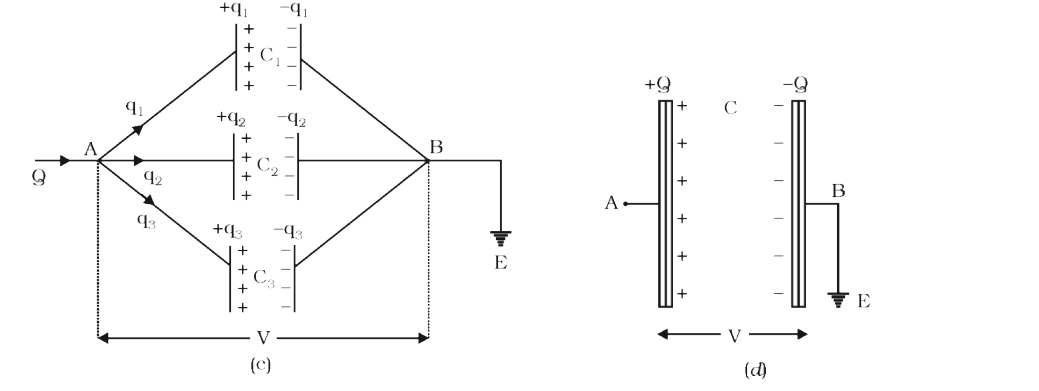
If in place of all the three capacitors, only one capacitor is placed between A and D such that on giving it charge Q, the potential difference between its plates become V, then it will be called equivalent capacitor. If its capacitance is C, then
`V=(Q)/(C)` . . (vi)
Comparing (v) and (vi) we get `(Q)/(C)=Q[(1)/(C_(1))+(1)/(C_(2))+(1)/(C_(3))]`
or `(1)/(C)=(1)/(C_(1))+(1)/(C_(2))+(1)/(C_(3))` . . (vii)
Thus in series arrangement, “The reciprocal of equivalent capacitance is equal to the sum of the reciprocals of the individual capacitors.”
Parallel Arrament: in fig (c) three

