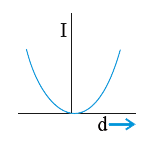
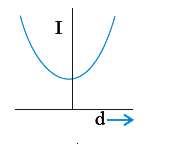
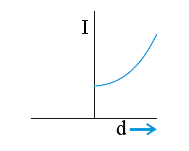
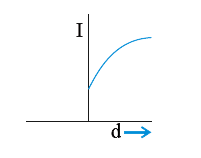
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
VMC MODULES ENGLISH|Exercise ENABLE|50 VideosSYSTEM OF PARTICLES AND ROTATIONAL MOTION
VMC MODULES ENGLISH|Exercise EFFICIENT|50 VideosSYSTEM OF A PARTICLES & ROTATIONAL MOTION
VMC MODULES ENGLISH|Exercise IN-CHAPTER EXERCISE F|10 VideosUNITS, MEASUREMENTS & ERRORS
VMC MODULES ENGLISH|Exercise IN - CHAPTER EXERCISE - B|10 Videos
Similar Questions
Explore conceptually related problems
VMC MODULES ENGLISH-SYSTEM OF PARTICLES AND ROTATIONAL MOTION-IMPECCABLE
- According to the theorem of parallel axes I = I("cm") + Mx^(2), the g...
Text Solution
|
- The angular momentum of body remains conserve if :
Text Solution
|
- A circular disc is to be made using iron and aluminium. To keep its mo...
Text Solution
|
- If rotational kinetic energy is 50% of total kinetic energy then the ...
Text Solution
|
- A person is standing on the edge of a circular platform, which is movi...
Text Solution
|
- A thin circular ring of mass M and radius r is rotating about its axis...
Text Solution
|
- A solid cylinder of mass M and radius R rolls without slipping down an...
Text Solution
|
- A bull rolls without slipping. The radius of gyration of the ball abou...
Text Solution
|
- The moment of inertia in rotational motion is equivalent to :
Text Solution
|
- Two rods each of mass m and length 1 are joined at the centre to form ...
Text Solution
|
- A wheel has moment of inertia 5 xx 10^(-3) kg m^(2) and is making 20 "...
Text Solution
|
- The ratio of the radii of gyration of a circular disc about a tangenti...
Text Solution
|
- A round disc of moment of inertia I2 about its axis perpendicular to i...
Text Solution
|
- Three particles, each of mass m are situated at the vertices of an equ...
Text Solution
|
- A wheel having moment of inertia 2 kg m^(2) about its vertical axis, r...
Text Solution
|
- In an orbital motion, the angular momentum vector is :
Text Solution
|
- A solid cylinder of mass 20kg has length 1 m and radius 0.2 m. Then it...
Text Solution
|
- A constant torque acting on a uniform circular changes its angular mom...
Text Solution
|
- A dancer is standing on a rotating platform taking two sphere on her ...
Text Solution
|
- The rate of change of angular momentum is called
Text Solution
|
- Two bodies have their moments of inertia I and 2I respectively about t...
Text Solution
|