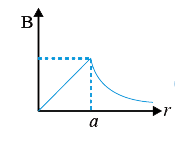
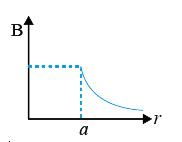
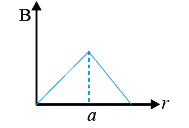
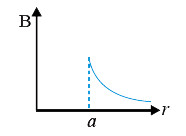
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
MOVING CHARGES & MAGNETISM
VMC MODULES ENGLISH|Exercise ENABLE|50 VideosMOVING CHARGES & MAGNETISM
VMC MODULES ENGLISH|Exercise EFFICIENT|50 VideosMotion in Two Dimensions
VMC MODULES ENGLISH|Exercise MCQ|2 VideosPROPERTIES OF MATTER
VMC MODULES ENGLISH|Exercise JEE Advanced (Archive) Level - 2 (MATRIX MATCH TYPE)|1 Videos
Similar Questions
Explore conceptually related problems
VMC MODULES ENGLISH-MOVING CHARGES & MAGNETISM -IN-CHAPTER EXERCISE-K
- The magnetic field due to a conductor fo unifrom cross section of radi...
Text Solution
|
- The angle of dip is the angle
Text Solution
|
- At a certain places, the angle of dip is 30^(@) and the horizon...
Text Solution
|
- The angle of dip at the magnetic equator is
Text Solution
|
- The line on the earth's surface joining the points where the field is ...
Text Solution
|
- The angle between the earths's magnetic and the earts's geographic axi...
Text Solution
|
- The lines joining the places of the same horizontal intensity are know...
Text Solution
|
- Direction of magnetic field at equatorial point
Text Solution
|
- The angle of dip at a place on the earth's surface gives
Text Solution
|
- At a certain place , horizontal component of earth's field is sqrt3 ti...
Text Solution
|
- At which place Earth's magnetic field becomes horizontal?
Text Solution
|