Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
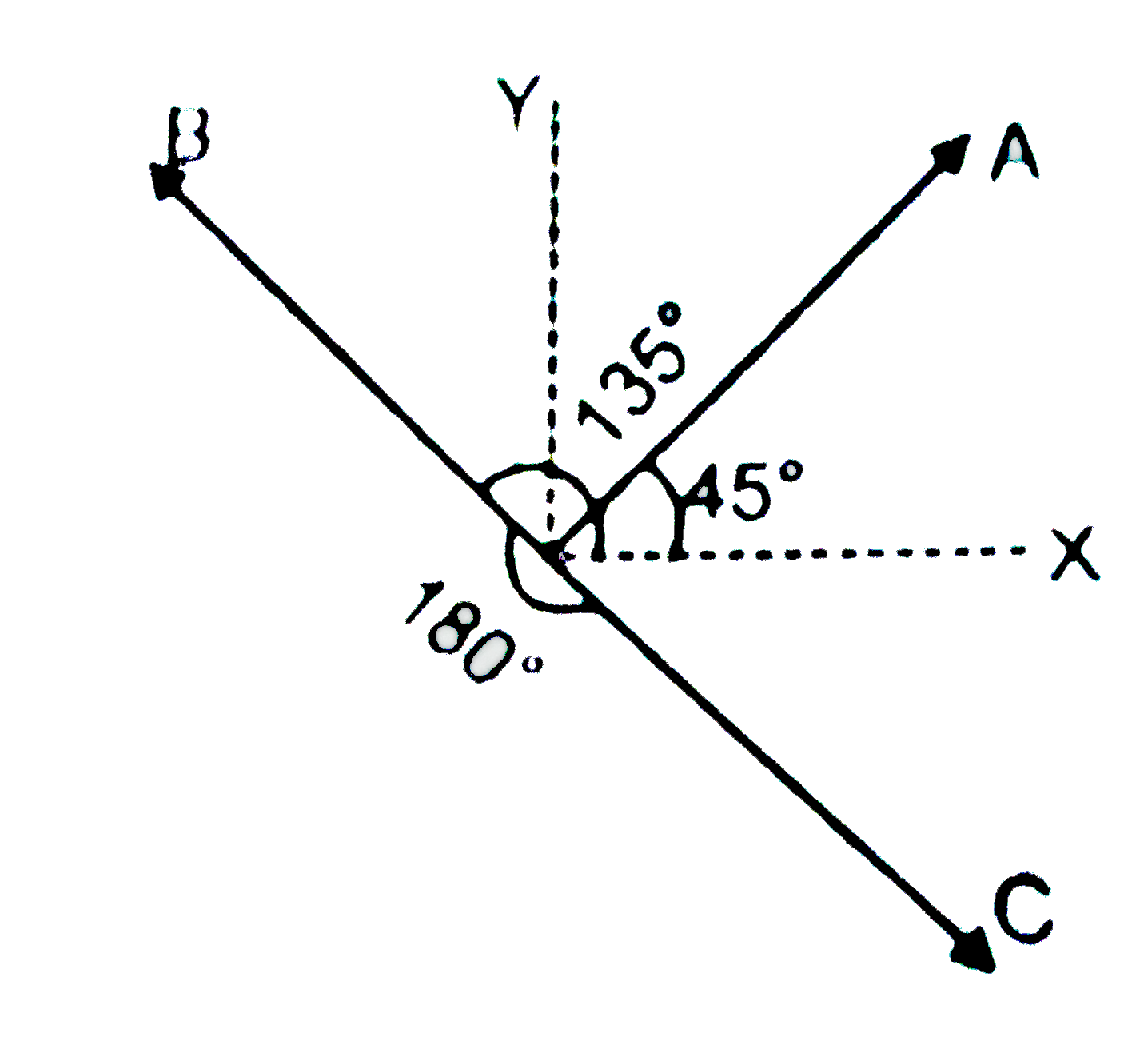
- Add vectors vecA,vecB and vecC which have equal magnitude s of 50 unit...
Text Solution
|
- If veca,vecb,vecc are mutually perpendicular vectors of equal magnitud...
Text Solution
|
- Add vectors vecA,vecB and vecC each having magnitude of 100 unit and i...
Text Solution
|
- The magnitudes of vectors vecA,vecB and vecC are 3,4 and 5 units respe...
Text Solution
|
- A magnitude of vector vecA,vecB and vecC are respectively 12, 5 and 13...
Text Solution
|
- यदि veca,vecb,vecc बराबर परिमाण के परस्पर लम्ब सदिश हो तो दिखाइए कि सद...
Text Solution
|
- यदि veca, vecb, vecc समान परिमाणों वाले परस्पर लंबवत् सदिश हैं तो दर्श...
Text Solution
|
- सदिशों vecA,vecB तथा vecC के परिमाण क्रमशः 3,4 तथा 5 इकाई है। यदि vecA...
Text Solution
|
- सदिश vecA,vecB तथा vecC का योग कीजिए। इन तीनों के परिमाण समान एवं 50 इ...
Text Solution
|