Text Solution
Verified by Experts
Topper's Solved these Questions
SYSTEM OF A PARTICLES & ROTATIONAL MOTION
VMC MODULES ENGLISH|Exercise SOLVED EXAMPLES|20 VideosSYSTEM OF A PARTICLES & ROTATIONAL MOTION
VMC MODULES ENGLISH|Exercise PRACTICE EXERCISE-1|4 VideosSIMPLE HARMONIC MOTION
VMC MODULES ENGLISH|Exercise 7-previous year question|46 VideosSYSTEM OF PARTICLES AND ROTATIONAL MOTION
VMC MODULES ENGLISH|Exercise IMPECCABLE|56 Videos
Similar Questions
Explore conceptually related problems
VMC MODULES ENGLISH-SYSTEM OF A PARTICLES & ROTATIONAL MOTION-IN-CHAPTER EXERCISE F
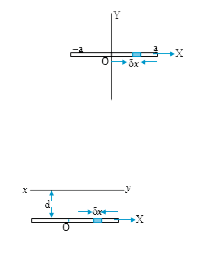
- A rod is of mass M = 3kg and length 2a (a = 2m). Find moment of inerti...
Text Solution
|
- A ball of radius 11 cm and mass 8 kg rolls from rest down a ramp of le...
Text Solution
|
- From an inclined plane a sphere, a disc, a ring and a shell are rolled...
Text Solution
|
- A solid cylinder 30 cm in diameter at the top of an inclined plane 2.0...
Text Solution
|
- A cylinder of mass M and radius R rolls on an inclined plane. The gain...
Text Solution
|
- A disc of radius R is rolling down an inclined plane whose angle of in...
Text Solution
|
- A solid cylinder (i) rolls down (ii) slides down an inclined plane. Th...
Text Solution
|
- The acceleration of a body rolling down on an inclined plane does not ...
Text Solution
|
- If a ring, a disc, a solid sphere and a cyclinder of same radius roll ...
Text Solution
|
- A ring is rolling on an inclined plane. The ratio of the linear and ro...
Text Solution
|
- The M.I. of a solid cylinder about its axis is I. It is allowed to roo...
Text Solution
|