Home
Class 12
PHYSICS
A wire of length l, mass m and resistanc...

A wire of length `l`, mass `m` and resistance `R` slides without any friction down the parallel conducting rails of negligible resistance . The rails are connected to each other at the bottom by a resistanceless rail parallel to the wire so that the wire and the rails form a closed rectangualr conducting loop. The plane of the rails makes an angle `theta` with the horizontal and a uniform vertical magnetic field of the inducetion `B` exists throughout the rregion. Find the steady state velocity of the wire.

Text Solution

Verified by Experts

Force down the plane = mg sintheta At any instant if the velocity is v the induced
Current in the loop -`(IB cos thetav)/(R)`
Force on the conductor in the horizontal direction  =`(nuBlcostheta)/(R)xxBxxl`
Component parallel to the incline =` (B^(2)l^(2)costheta)/(R)xxvxxcostheta`
If v is constant this force should be angle to mg sin thetatherefoer `v=(mRgsintheta)/B^(2)l^(2)cos^(2)theta)`
Promotional Banner

Topper's Solved these Questions

  • ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT

    VMC MODULES ENGLISH|Exercise SOLVED EXAMPLES|24 Videos

  • ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT

    VMC MODULES ENGLISH|Exercise PRACTICE EXERCISE 1|10 Videos

  • DYNAMICS OF A PARTICLE

    VMC MODULES ENGLISH|Exercise JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )|31 Videos

  • ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT

    VMC MODULES ENGLISH|Exercise IMPECCABLE|52 Videos

Similar Questions

Explore conceptually related problems

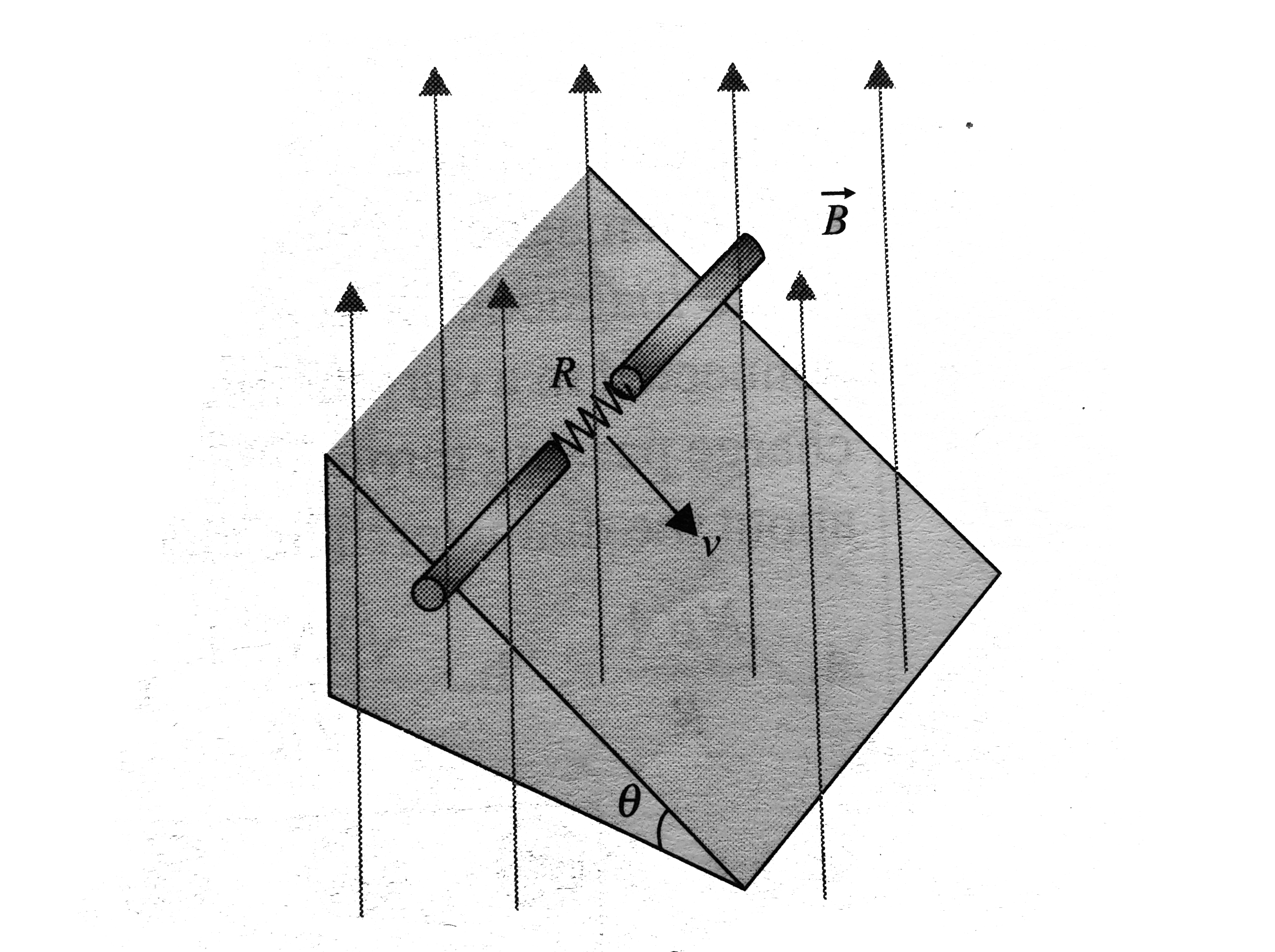
A wire of length l, mass m and resitance R slides without any friction down the parallel conducting rails of negligible resistance (Fig). The rails are connected to the wire so that the wire and the rails form a closed rectangular conducting loop. The plane of the rails makes an angle theta with the horizontal and a uniform vertical magnetic field of induction B exists throughout the region. Find the steady-state velocity of the wire

A wire cd of length l and mass m is sliding without friction on conducting rails ax and by as shown. The verticle rails are connected to each other with a resistance R between a and b . A uniform magnetic field B is applied perpendicular to the plane abcd such that cd moves with a constant velocity of

A wire ab of length l, mass m and resistance R slided on a smooth, thick pair of metallic rails joined at the bottom as shown in . The plane of the the rails makes an angle theta with the horizontal. A vertical magnetic field B exists in the ragion. if the wire slides on the rails at a constant speed v, show that B = sqrt(mg R sin theta)/(vl^2 cos^theta) .

A conducting wire of length l and mass m can slide without friction on two parallel rails and is connected to capacitance C . The whole system lies in amagnetic field B and a constant force F is applied to the rod . Then

A conducting wire of length l and mass m can slide without friction on two parallel rails and is connected to capacitance C . Whole system lies in a magnetic field B and a constant force F is applied to the rod. Then

A conducting rod of length L slides at a constant velocity V on two parallel conducting rails as shown in figure. The mechanical power required to pull the rod at constant velocity is

A wire of mass m and length I can freely slide on a pair of parallel, smooth, horizontal rails placed in a vertical magnetic field B . The rails are connected by a capacitor of capacitance C. The electric resistance of the rails and the wire is zero. If a constant force F acts on the wire as shown in the figure, find the acceleration of the wire.

A pair of parallel conducting rails lie at right angle to a uniform magnetic field of 2.0T as shown in the fig. two resistor 10Omega and 5Omega are to slide without friction along the rail. The distance between the conducting rails is 0.1m . Then

A rod of mass m and resistance r is placed on fixed, resistanceless, smooth conducting rails (closed by a resistance R ) and it is projected with an initial velocity u .Find its velocity as a function of time.

A copper rod of mass m slides under gravity on two smooth parallel rails l distance apart set at an angle theta to the horizontal. At the bottom, the rails are joined by a resistance R . There is a uniform magnetic field perpendicular to the plane of the rails. the terminal valocity of the rod is