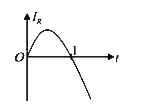
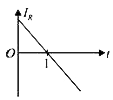
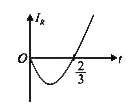A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
VMC MODULES ENGLISH-MOCK TEST 11-Physics (Section-2)
- A long solenoid of radius R carries a time (t)-dependent current I(t)=...
Text Solution
|
- A Carnot’s engine operates with an efficiency of 40% with its sink at ...
Text Solution
|
- A hollow aluminium cylinder 20.0 cm deep has an internal capacity of 2...
Text Solution
|
- A particle (m=1kg) slides down in frictionless-track AOC starting from...
Text Solution
|
- A loop has two semi-circular arcs of radii R (= (5)/(sqrtpi) m) each...
Text Solution
|
- The threshold frequency of a certain metal is 3.3xx10^(14)Hz. If light...
Text Solution
|