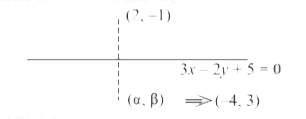Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
VMC MODULES ENGLISH-JEE MAIN - 5-PART III : MATHEMATICS (SECTION-2)
- The number of common tangents to the circle x^(2)+y^(2)-2x-4y-4=0 and ...
Text Solution
|
- In a circle with centre 'O' PA and PB are two chords. PC is the chord...
Text Solution
|
- In a triangle A B C , if A is (2,-1),a n d7x-10 y+1=0 and 3x-2y+5=0 ar...
Text Solution
|
- If (2, 1), (-1, -2), (3, -3) are the mid points of the sides BC, CA, A...
Text Solution
|
- The point of tangency of the circles x^2+ y^2 - 2x-4y = 0 and x^2 + y^...
Text Solution
|