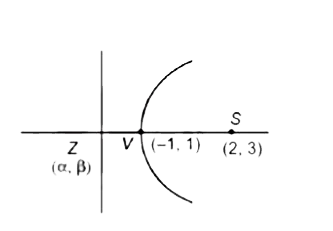A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- vertex and focus of a parabola are (-1,1) and (2,3) respectively. find...
Text Solution
|
- FInd the equation of the parabola The focus at (1,1) the directrix x-y...
Text Solution
|
- Find the equation of the parabola having focus (1, 1) and vertex at (-...
Text Solution
|
- vertex and focus of a parabola are (-1,1) and (2,3) respectively.find ...
Text Solution
|
- The vertex of the parabola whose focus is (-1,1) and directrix is 4x +...
Text Solution
|
- Find the equation of the parabola with vertex (2,3) and focus (0,5).
Text Solution
|
- The equation of the parabola with its vertex at (1,1) and focus at (3,...
Text Solution
|
- Find the equation of parabola whose focus is (0,1) and the directrix i...
Text Solution
|
- Find the co-ordinates of the vertex and focus the equation of the dire...
Text Solution
|