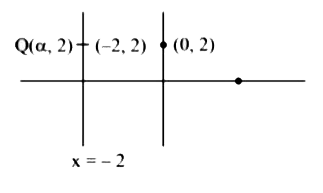A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- The mirror image of the focus to the parabola 4(x + y) = y^(2) w.r.t....
Text Solution
|
- Find the equation of the parabola whose focus is (-3,2) and the direct...
Text Solution
|
- Write the equation of the parabola with focus (0,0) and directrix x+y-...
Text Solution
|
- Find the vertex, focus and directrix of the parabola x^(2)=2(2x+y).
Text Solution
|
- Find the vertex, focus and directrix of the parabola x^(2)=2(2x+y).
Text Solution
|
- The mirror image of the focus to the parabola 4(x + y) = y^(2) w.r.t....
Text Solution
|
- The equations of the parabola with focus (0,0) and directrix x+y=4, is
Text Solution
|
- If focus and directrix of a parabola are (3,5) and x+y=4, then coordin...
Text Solution
|
- The equation or the parabola with focus (0, 0) and directrix x+y = 4 i...
Text Solution
|